Inscription / Connexion Nouveau Sujet
Mécanique
Bonjour
(à Regerder Dessin)
Il me faut désigner l'énergie potentille du système {Poulie, m, M}
les axes (O'x) (Oy) coïncident avec les positions G1 et G2 (centres d'inertie de m et M) à l'équilibre du système. A t=0 on écarte M aux bas à partir de sa position d'équilibre.
les plans horizontaux passant par O et O' comme références de l'énergie potentielle de pesanteur respectivement pour M et m, la référence de l'énergie P élastique est prise quand le ressort n'est pas déformé.
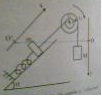
Peut-être parce qu'on n'arrive pas à bien distinguer les détails du dessin ?
Et donc au risque de se tromper :
Supposant R le rayon de la grande poulie et r le rayon de la petite.
Au repos :
La somme des moments des forces autour de l'axe de rotation commun des poulies est nulle :
MgR - mgr.sin(alpha) - k.r.Delta Lo = 0
(k est la constante élastique du ressort et Delta Lo son allongement au repos (masse M et m immobiles)).
k.r.Delta Lo = MgR - mgr.sin(alpha)
Delta Lo = (g/k).(MR/r - m.sin(alpha))
Et donc le zéro pour l'énergie élastique du ressort est en x = -(g/k).(MR/r - m.sin(alpha))
-----
Lorsque G1 est à l'abscisse x, G2 est en y = x.R/r
Energie potentielle de pesanteur de m : Ep1 = m.g.x.sin(alpha)
Energie potentielle de pesanteur de M : Ep2 = -M.g.y = -M.g.x.R/r
Energie potentielle élastique du ressort : Ep3 = (1/2).k.(Delta L)² = (1/2).k.[x + (g/k).(MR/r - m.sin(alpha))]²
Energie potentielle totale (ressort + M + m) en fonction de x : Ep = m.g.x.sin(alpha) - M.g.x.R/r + (1/2).k.[x + (g/k).(MR/r - m.sin(alpha))]²
-----
Rien relu et donc tu as intérêt à tout vérifier.

pour la poulie, il n'y a pas d'energie de pesanteur?
Evidemment non.
Par contre, si on doit ensuite étudier le mouvement d'oscillation, il faudrait tenir compte de l'énergie cinétique de la poulie (1/2.J.w²), sauf si l'énoncé précise qu'on peut négliger J (moment d'inertie de la poulie autour de son axe) dans l'étude.

Bah comment trouver l'energie potentielle de pesanteur de la poulie si on a pas sa masse et son (J est déterminée dans l'énoncée et non négligée)
la poulie ne bouge pas (elle reste donc à la même hauteur et son Epp ne varie pas, donc tu prends Epp(poulie) = 0 par convention et le tour est joué!


