Inscription / Connexion Nouveau Sujet
mécanique
bonjour voici un exercice de mécanique qui me pose problème:
1) Deux ressorts identiques de longueur à vide l0 et de raideur k sont accrochés à deux points points distants de d situés sur une même horizontale. On relie leurs extrémités libres et on y accroche un objet de masse m.
Les ressorts font alors un angle 
par rapport à la verticale.
A l'aide d'une étude mécanique complète, déterminer une expression reliant , d, lo, k, m et l'intensité de pensanteur g.
Application numérique : calculer avec k = 10 N.m-1, d = 20cm, lo = 10 cm, m = 200g et g = 9.8 N/kg
Dans l'ordre:
- on étudie un objet dans un référentiel terrestre supposé galiléen
-bilan des forces:
son poids P
verticale vers le bas de norme P = mg
parcontre pour la force de tension du ressort , comme le ressort à la même raideur et même longueur à vide les deux ressorts exercent une norme de même force non? L'objet serai alors equidistant des points fixes du ressorts
Merci d'avance pour toute aide^^
Faire un dessin:
Soit T la force de rappel d'un des ressorts. (pareil évidemment pour l'autre ressort)
Soit P le poids de l'objet.
Soit L la longueur d'un ressort.
Projection sur un axe vertical des forces agissant sur l'objet :
P = 2T.cos(theta)
mg = 2T.cos(theta)
relation géométrique :
d/2 = L.sin(theta)
et L = Lo + T/k
-----
Il reste donc à éliminer L et T entre les 3 équations:
mg = 2T.cos(theta)
d/2 = L.sin(theta)
L = Lo + T/k
d/2 = (Lo + T/k).sin(theta)
d.k = 2.(k.Lo + T).sin(theta)
Et T = mg/(2.cos(theta))
d.k = 2.(k.Lo + mg/(2.cos(theta))).sin(theta)
d.k = (2.k.Lo.cos(theta) + mg).tan(theta)
-----
Vérifie. 
bonjour et merci
désolé pour le retard^^:
J-P:
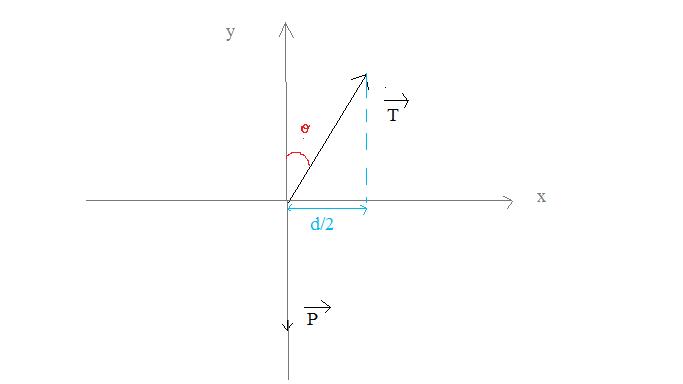
On ne devrait pas plutôt projeter les forces sur un axe (o;
;
)?
puisque la force de rappel du ressort n'est pas nul sur x non?
à J-P et geegee
vous trouver ses égalités en projetant les forces sur l'axe ci-dessous? Car moi j'en trouves certaine avec le même
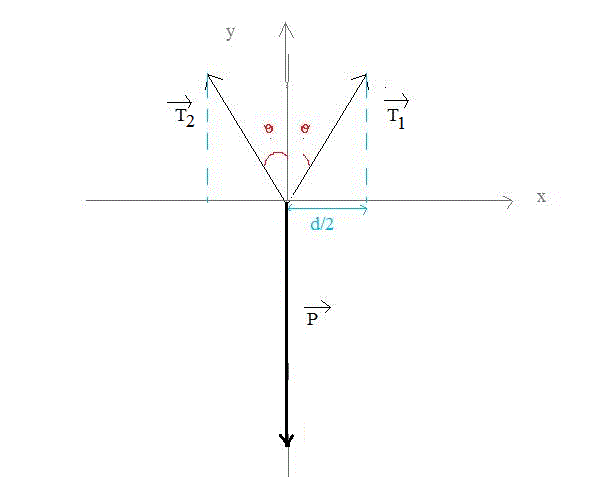
En projetant sur l'axe vertical : P = T1.cos(theta) + T2.cos(theta)
|T1| = |T2| puisque les 2 ressorts sont identiques.
--> P = 2.T1.cos(theta)
mg = 2.T1.cos(theta)
-----
En appelant L la longueur étirée d'un des ressorts, on a aussi : d/2 = L.sin(theta)
-----
T1 est la force exercée par un des ressort et donc T1 = k.(L - Lo)
-----
On a donc 3 équations :
mg = 2.T1.cos(theta)
d/2 = L.sin(theta)
T1 = k.(L - Lo)
Il reste donc à éliminer L et T entre ces 3 équations pour trouver une expression reliant theta , d, lo, k, m et g.
C'est ce qui a été fait dans mon premier message.
-----
Il n'est nul besoin ici d'aussi projeter les forces sur l'axe horizontal ... si ce n'est pour montrer ce qui est évident soit que |T1| = |T2|
Sauf distraction.
bonjour et merci!
j'ai une petite question: pour l'étude mécanique on a utilisé la première loi de newton mais dans l'énoncé qu'est-ce-qui nous permet de l'utilisé?
d.k = (2.k.Lo.cos(theta) + mg).tan(theta)
ce n'est pas plutôt d.k = (2.k.Lo.sin(theta) + mg).tan(theta)??
pour l'application numérique avec le solver de la calculatrice je trouve plusieur valeurs à
à la fois négative et positive comment savoir laquelle est la bonne?d.k = (2.k.Lo.cos(theta) + mg).tan(theta)
et
d.k = (2.k.Lo.sin(theta)) + mg.tan(theta)
C'est la même chose ... si on comprend bien l'usage des parenthèses.
-----
« Tout corps persévère dans l'état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n'agisse sur lui, et ne le contraigne à changer d'état. »
... Sous entendu dans un référentiel Galiléen.
Dans le problème posé, on peut considérer que le réferentiel terrestre est Galiléen.
Comme l'objet est au repos dans un référenriel terrestre, on peut donc conclure que la résultante des forces agissant sur l'objet est nulle.
Donc, la somme des projections sur un axe quelconque (dans le référentiel terrestre) des forces agissant sur l'objet est nulle.
Les 3 forces agissant sur l'objet, sonr son poids P et T1 et T2 qui sont exercée par les ressorts sur l'objet.
La somme vectorielles de P, T1 et T2 est nulle.
La somme des projections sur un axe horizontal de ces 3 forces est nulles aussi. (1)
La somme des projections sur un axe vertical de ces 3 forces est nulles aussi. (2)
(1) permet d'écrire que |T1| = |T2|
et (2) permet alors de trouver que : |P| = 2.|T1|.cos(theta)
Des considérations purement géométriques permettent aussi de dire que : d/2 = L.sin(theta)
Et par la relation connue pour les ressort, on a aussi : |T1| = k.(L - Lo)
Et donc ...
très bien merci,
donc:
d.k = (2.k.Lo.sin(theta)) + mg.tan(theta)
pour la valeur numérique je trouve plusieurs valeurs à ???
comment savoir laquelle prendre 
Annuler
connectez vous