Inscription / Connexion Nouveau Sujet
Meca: Force non conservatrice
Bonjour,
j'aurais besoin d'aide pour une question d'un exercice, alors,
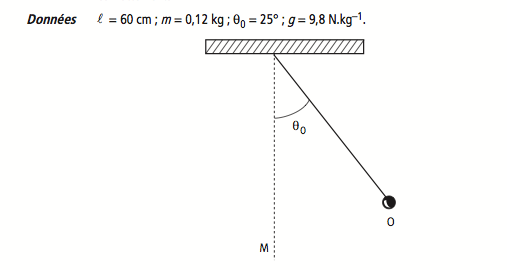
Exprimer le travail de la force (vec)T exercée par le fil W(vec)T en fonction de m, de g, de l et de  0 lorsque la bille passe de O en M. Calculer sa valeur.
0 lorsque la bille passe de O en M. Calculer sa valeur.
Donc je sais que la force exercée par le fil est une force non conservatrice, par contre quelle formule dois-je utilisé pour la calculer, une piste svp ? Merci bien
bonjour,
mon frère qui est proprio du compte de Titop vient de se faire bannir par l'autobann car il utilise la même IP que moi..
Enfin bref pas juste ce système, voila il continuera de vous parler via ce compte.
Si le fil reste tendu, la bille se deplace perpendiculairement au fil oui, et donc on aura un produit scalaire nul..
Ce qui fait que W(vec)T = 0 ?
Dois-je juste expliquer comme ça?
Oui le travail de la tension est nul car celle-ci reste toujours perpendiculaire au mouvement. On dit que la tension ne travaille pas.
Ainsi les seules forces qui travaillent sont des forces conservatives et l'énergie mécanique se conserve.
Oui ok, le travail est nul, mais cependant, comment je ne repond toujours pas a la question qui est :
"exprimer" le travail de la force. Dois-je juste faire :
 W(vec(T)) = 0.. ?
W(vec(T)) = 0.. ?
Dans une base polaire ,
et en appelant A le point d'attache du fil au mur,
.
Le travail élémentaire vaut :
Le travail entre O et M vaut :
Mais on peut se restreindre à écrire :
Bonjour,
merci beaucoup de m'avoir aidé à l'exprimer.
Cependant une autre question me tracasse un peu.
Le pendule s'arrête d'osciller après plusieurs oscillations. Comment expliquez-
vous le fait qu'il s'arrête d'osciller ?
Sachant qu'il n y a pas de frottements, j'ai creusé, creusé puis j'ai fais un petit paragraphe expliquant que la tension du fil au point A dissipait un peu d'énergie, ce qui fait que le pendule s'arrête d'osciller après beaucoup beaucoup d'oscillations :p voila en gros c'est ça.
Vous en pensé quoi?
Bonjour,
c'est exactement ça : il y a des frottements au point d'attache A. On peut aussi considérer des frottements avec l'air, mais dans le cadre d'un pendule comme celui-ci, les frottements dus au point d'attache sont bien supérieurs aux frottements avec le fluide.



