Re bonjour,
j'avance doucement ...
Def cours issu du livre:
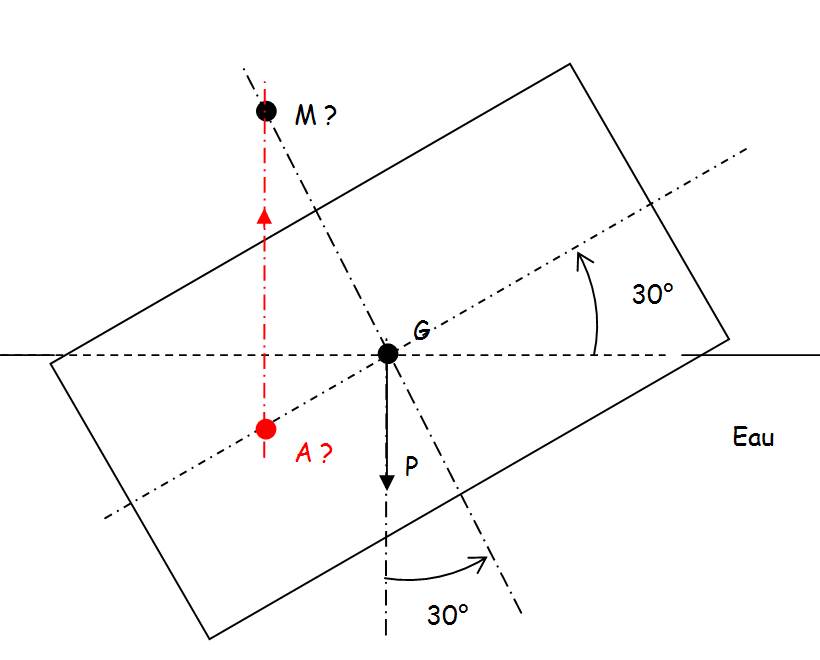
"Le point M situé  à l'intersection de la verticale passant par A et de l'axe de symetrie est appelé métacentre,
si M est situé au desssus de G il y a tjrs stabilité ; le solide tend à revenir dans sa position équilibre &apres un écart. Il y a instabilité dans le cas contraire, lorsque M est au dessous de G.

Il me reste plus qu'a chercher comment trouver le point A centre de poussé...

May day,may day,....

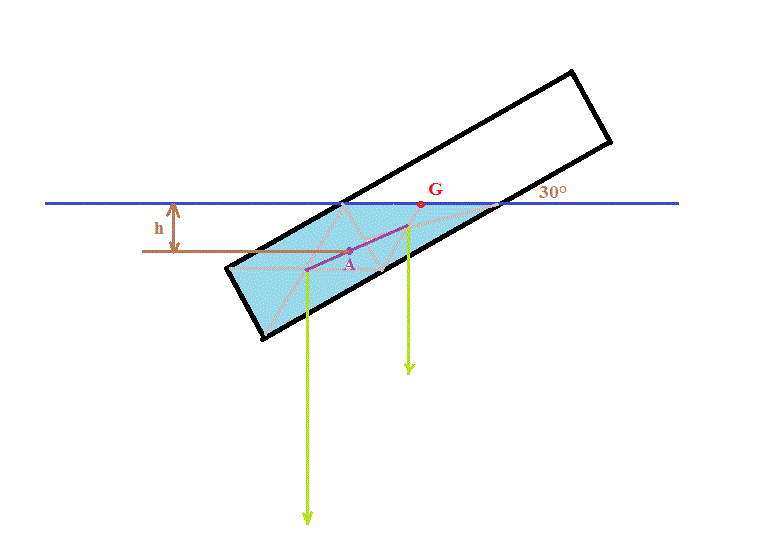
A est le centre de gravité géométrique de la partie immergée.

Pour trouver sa position, on peut découper la partie sous eau en plusieurs morceaux (ex sur la coupe dessinée, un triangle et un rectangle).
Et rechercher le centre de gravité (géométrique) de ces différentes parties et puis rechercher le centre de gravité de toute la partie sous eau (en bleu clair) en combinant les positions des centres de gravités des différentes parties (triangle et rectangle) en tenant compte évidemment de leurs "poids" respectifs.
En le faisant graphiquement pour 30°, on a, à peu près, ce que j'ai dessiné.
Et en mesurant sur le dessin, on a la différence d'altitude entre A et G d'environ 104 mm.

Il faudrait le refaire en calculant au lieu de graphiquement seulement, mais le principe reste le même.

Enfin, il me semble que c'est cela qui est demandé dans la partie 2 de l'exercice.

Merci JP, pour ton aide.
Ta façon d'expliquer est tres claire, c'est un plaisir d'avoir lu ta reponse.
Je me reserve plus de temps pour la resolution analytique demain matin, car je viens d'essayer et j'ai un peu de mal. Les angles m'inquietent un peu ...
Merci

Bonjour
je n'arrive pas à calculer les coordonnées des différents points de la figure (rectangle et triangle). Je suis alors bloqué.
je travaille dans le plan (Y;Z), soit
A(200;100)
B(-200;100)
C(-200;-100)
D(200;100).

si je prends petit "a" : centre de gravite de la surface immergée situé quelque part sur G1 et G2
Yga = [(Yg1.S1)+(Yg2.S2)] / (S1+S2)
Zga = [(Zg1.S1)+(Zg2.S2)] / (S1+S2)
avec S1 = (E'F'.F'H')/2 et S2 = C'D'.D'E'

Merci de me remettre sur le bon chemin ...

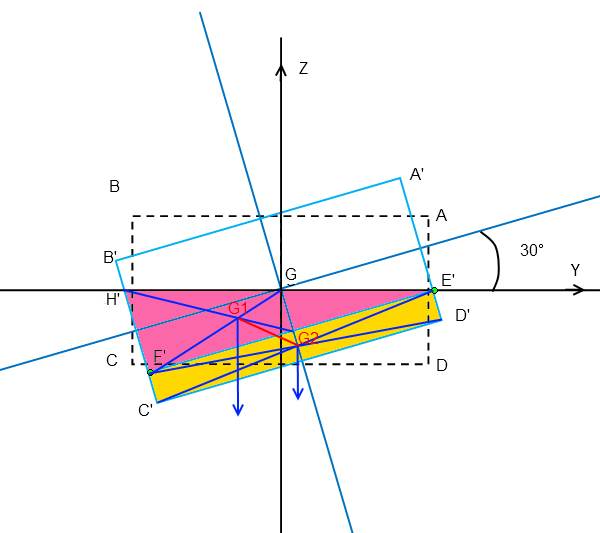
Je fais celui avec 30°



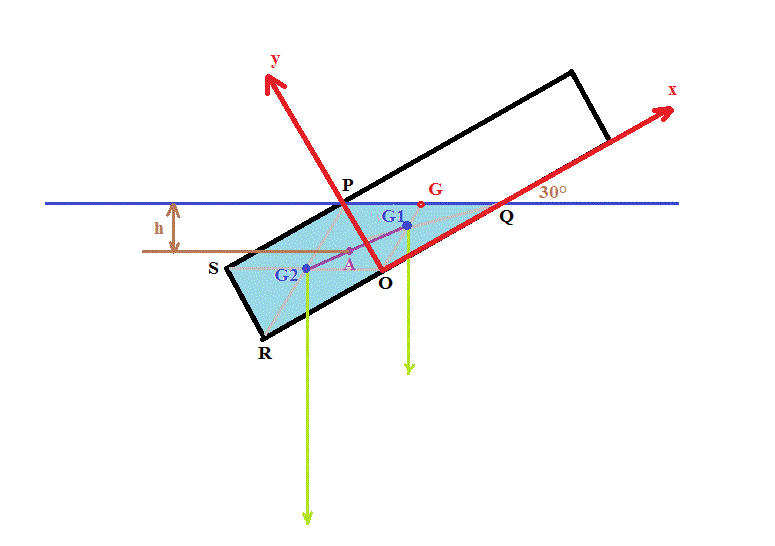
Choix du repère comme dessiné.

Avec 30°

L'aire du triangle OPQ est A1 = (1/2) * 200 * 200/tg(30°) = 20000/tg(30°) = 34641
L'aire du rectangle OPSR est A2 = 200 * (1000 - 2*200/tg(30°)) = 200000 - 8000/tg(30°) = 61436

Coordonnées des sommets du triangle : (0;0) , (0;200) , (200/tg(30°) ; 0)
G1(200/(3.tg(30°)) ; 200/3)
G1(115,47 ; 66,67)

G2(-(1000 - 2*200/tg(30°))/2 ; 100)
G2(-153,59 ; 100)

A est le centre de gravité de G1 et G2 pondérés par le poids des aires A1 et A2

Abscisse de A : (115,47 * 34641 - 153,59 * 61436)/(34641 + 61436) = -56,58
Ordonnée de A : (66,67 * 34641 + 100 * 61436)/(34641 + 61436) = 87,98

A(-56,58 ; 87,98)

Equation de l'horizontale passant par G et donc aussi par les points (0;200) , (200/tg(30°) ; 0)

200 = b
0 = a*200/tg(30°) + 200
a = tg(30°)
---> la droite : tg(30°).x - y + 200 = 0

h est la distance entre le point A(-56,58 ; 87,98) et la droite d'équation tg(30°).x - y + 200 = 0

h = |-56,58*tg(30°) + 87,98*(-1)|/V(tg²(30°) + 1²)

h = 104 mm
-----
Sauf distraction.  

Merci pour ta reponse si rapide.
J'ai du mal a comprendre certain calcul de distance. Il me faut plus de temps pour reflechir,et je ne pourrais m'y remettre que demain matin. en attendant je te remercie sincerement.

Bonjour
Je ne comprends pas comment tu calcules l'aire du rectangle A2.

L'aire du rectangle OPSR est A2 = 200 * (1000 - 2*200/tg(30°)) =  61436

200 = OP pas de probleme.
(1000 - 2*200/tg(30°)) = OR là, je ne comprends pas comment tu calcules OR ou PS.

De plus, je remarque autre chose, la modelisation de nos boites n'est pas la même, pourtant elles sont à 30° toutes les deux (mon schéma est à l'echelle). J'ai pivoter ma boite autour de G sur l'axe de symetrie dans le sens trigonometrique. nos decompositions en surfaces de base sont differentes.
Mon B' correspond à ton S
B' est au dessus de l'eau alors que S est immergé,  G est situé sur la ligne de flottaison dans les deux cas.
Les deux solutions sont elles bonnes, j'ai du mal à le croire.?

rebonjour,
j'ai compris, tu as pris une boite de longueur AB = 1000, alors que pour moi AB = 400 (sur mon schéma).

Revenons à ta modelisation:
G se situe au milieu de PQ, alors la projection ortho de G sur OQ est au milieu de OQ qui est le milieu de la longueur.
reste plus qu'a soustraire OQ de la longueur totale (1000 pour toi et 400 pour moi) et diviser par 2 por trouver RO.

Ce n'est évidemment pas la même chose d'incliner de 30° les arètes de 1000 ou les arètes de 400.

Le résultat (calcul de h) est forcément différent dans les 2 cas.

Il semble plus "naturel", même si cela ne signifie par grand chose, d'incliner les arètes de 1000 qui est la plus grande longueur. Par contre, je suis sûr que c'est comme cela que l'auteur de la question l'a pensé (il aurait mieux fait de l'écrire explicitement) ... puisque la réponse du corrigé (h = 104 mm pour inclinaison de 30°) colle avec ce qu'on trouve en considérant les arètes de 1000 inclinée des angles donnés.

Merci encore JP.
Effectivement l'orientation et le choix du repere sont importants.
J'ai trouvé la formule qui donne la distance entre un point et une droite que je ne connaissais pas.
Pour moi L'équa de notre ligne de flottaison est y = ax + b.
Je suis surpris de voir qu'il me faut travailler avec une equation de la forme ax +by +c =0 comme tu le fais, mais ensuite en appliquant la formule je me reconcilie avec la fin du td.
je te remercie pour toutes tes explications et le temps que tu m'as consacré.
Je continue alors ma série de TD ...en tentant de m'améliorer en meca des fluides
A bientot