Inscription / Connexion Nouveau Sujet
Lois de Newton
Bonjour,
j'ai quelques difficultés en ce qui concerne les Lois de Newton. Donc je fais un exercice en ce moment qui me pose problème, et j'aimerais avoir quelques conseils. J'ai déjà commencé l'exercice, je vous abrège mes réponses, histoire que vous ayez une idée de ce que j'ai fais, bref toute aide ne sera pas de refus  .
.
On étudie une petite bille de masse m que l'on assimile à un point.
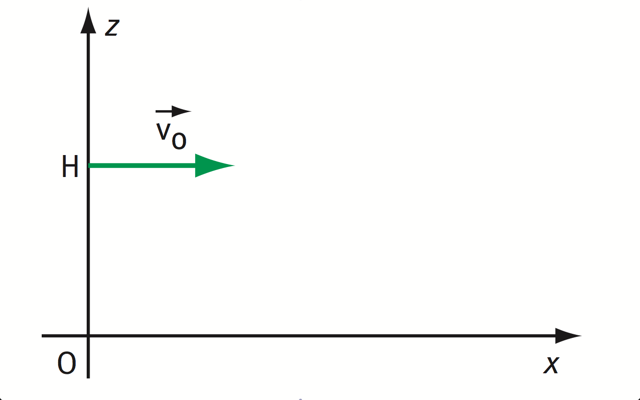
À t = 0 s, on la lance avec une vitesse horizontale de valeur v0 = 1,8 m.s-1, à la hauteur zt=0 = H = 60 cm, au-dessus du sol.
On suppose que le mouvement a lieu dans le plan xOz, avec Oz : axe vertical dirigé vers le haut et Ox : axe horizontal de même direction que le mouvement de la bille.
On note le champ de pesanteur g = 9,8 m.s-1.
Les effets de l'air sur la bille sont négligés.
1 Déterminer les coordonnées ax et az du vecteur accélération.
2 En déduire les coordonnées de la vitesse.
3 Donner l'expression des composantes verticale et horizontale du vecteur vitesse v.
4 En déduire les équations horaires du mouvement.
Mes réponses :
1) après avoir donné le système, présenté le référentiel, montré les forces soumise à la bille, et annoncé la 2e Loi de Newton, j'ai déduis grâce au doc que : g(0; 0; [vecteur]-g ) ; [vecteur]a (ax; ay; az)
et donc que :
ax=0
az=-g
Si je ne me trompe pas il n y a pas d'unité pour ces résultats?
2)
Vox = vecteur Vo
Voz = -g
Je ne vois pas ce que je pourrais mettre d'autre ici? à par expliquer pourquoi j'ai choisis ces réponses ?
3) Je sais que la dérivée du mouvement = l'accélération.
Donc j'utilise un truc de ce genre, que j'ai déduis d'autres exercices sans vraiment comprendre pourquoi..
ax=dVx/dt = 0 ==> V x (t) = constante.
Vox = [vecteur]Vo
az[/sub= dV[sub]z/dt =-g ==> Vz x (t) = -gt x cste ==> cste = -g
Alors la, je ne comprend meme pas ce que je fais, je suis pas du tout persuadée de ces resultats... D'ailleurs je ne les comprends meme pas.. J'ai juste essayé :/.
4) Je sais que la dérivée de l'accélération = vitesse.
Vx = dx/dt = Vo ==> x (t) = Vo x 0 + cste = 0.
Franchement à partir de là je suis perdu, j'aimerais juste quelques explications des questions du genre ce qu'on attend de moi, et ce que je dois faire pour y arriver, je sais que si je comprend cet exercice, tous les autres se ressembleront à peu près. J'ai beau lire mon cours, le corrigé d'exercice, ça ne veut pas rentrer dans ma tête.
Merci d'avance pour vos réponses.
hello
1) très bien, évidemment pas d'unité puisque tu es en littéral.
2) autant dire que je ne comprends pas la différence entre la question 2 et la question 3. En tout cas je préfère parler des composantes des vecteurs a et v plutot que des coordonneés.
comme tu l'as dit, dv/dt = a. c'est valable sur chaque axe dans ce repère donc dvx/dt = ax = 0 et dvz/dt = az = -g
maintenant tu intègres :
dvx/dt = 0 implique que vx = constante1. dans notre cas, constante1 = Vo
dvz/dt = -g implique que vz = -g.t + constante2. dans notre cas, constante2 = 0
ça va mieux ?
Bonjour,
Tout d'abord merci pour ta réponse, je pense comprendre un peu, ça rentre petit à petit.
4) pour les équations horaire je pensais à intégrer Vx et Zx.
Ça donnerais quelque chose du genre
x(t) = x + constante1
et
z(t) = -1/2 gt2 + constante2
Bonjour,
est-ce que je pourrais avoir plus de détails sur la procédure de ces calculs J-P, je n'arrive pas trop à comprendre comment vous avez procédé.
Merci pour votre réponse
Salut,
efpe t'a écris
dvx/dt = 0 implique que vx = constante1. dans notre cas, constante1 = Vo
dvz/dt = -g implique que vz = -g.t + constante2. dans notre cas, constante2 = 0
tu as répondu
4) pour les équations horaire je pensais à intégrer Vx et Zx.
Ça donnerais quelque chose du genre
x(t) = x + constante1
et
z(t) = -1/2 gt² + constante2
z(t) est juste mais x(t) est faux car tu fais une confusion entre le x de f(x) des mathématiciens et le x de x(t) des physiciens
dx/dt= Vo
dz/dt = -g.t
on intègre par rapport à t
donc x(t)=Vo*t+cste
et z(t)=-gt²/2 + cste2
(en maths on aurait f'(x)=k => f(x)=kx+cste et g'(x)== -m.x => g(x)=-mx²/2+cste)
En maths ce n'est pas dérangeant de laisse les constantes car quand on intègre une fonction on obtient une infinité de primitives
Mais en physique on cherches la position réelle d'un objet, donc on garde la primitive qui passe par le point connue
x(t)=Vo*t+cste
donc x(0)=Vo*0+cste
donc x(0)=cste
or x(0)=0
donc cste=0
on sait que quand t=0 x(t)=x(0)=0
Bonjour,
merci à vous, et vos réponses très clair, je comprend mieux maintenant. Je suis actuellement entrain de répondre à d'autres questions, je vous fais signe si j'ai des difficultés.
Merci encore.
bonjour j'ai le même exercice, mais je ne comprends pas pourquoi dans la 1ere question az= -g puisque la direction de la bille est dans le sens de 0x et non de 0z. j'aurais mis comme valeur az=0



