Inscription / Connexion Nouveau Sujet
Loi horaire
J'ai un exercice que j'ai eu en devoir que je n'arrive pas à résoudre entièrement malgré mon cours...
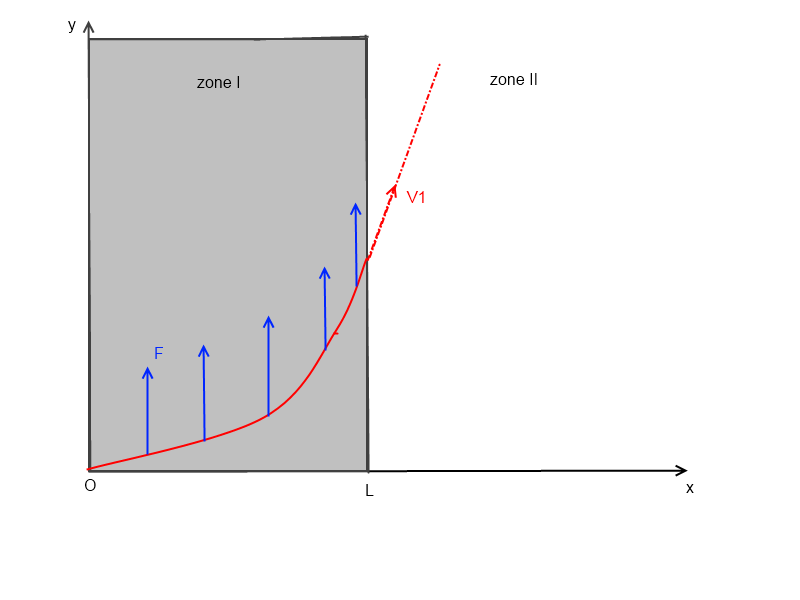
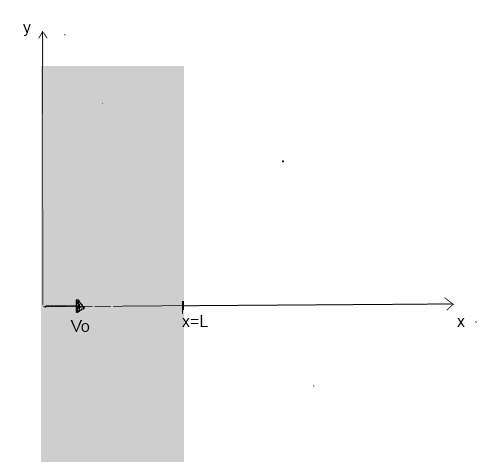
Sur le dessin ci contre une particule de masse m rentre dans la région grisée avec une vitesse V0ok ( selon Ox). La région grisée dite région I a une largeur L dans la direction Ox et s'étend à l'infini selon y. Quand la particule est dans cette région grisée, elle est soumise à une force F constante dirigée selon l'axe Oy. Si la particule sort de la région grisée ( région II ), elle n'est plus soumise à aucune force.
(i) Déterminez les lois horaires de la particule x(t) et y(t) dans région I. Déterminer ensuite la trajectoire y(x) et l'ordonnée y1 atteinte en x=L
Alors je pose ax(t)=0 et ay(t)=-g, comme la particule est soumise a une seule force elle est en chute libre
ce qui donne ensuite vx(t)=v0x=cste et vy(t)=-gt+v0y
et enfin x(t)=vox*t+x0 et y(t)=-1/2gt²+v0y*t+y0
pour déterminer la trajectoire je pose t=x-x0/v0x mais je vois pas ça va etre n'importe quoi si je remplace dans y... Mais on a aucune valeur... Je sais pas trop que faire.
(ii) Déterminer la trajectoire de la particule dans la région II lorsque la particule est sortie de la région I. Commentez la trajectoire obtenue.
J'y es réfléchie mais je préfère répondre entièrement à la première question avant de voir le reste.
Merci de votre aide 
comme la particule est soumise a une seule force elle est en chute libre
non,
un corps est en chute libre lorsqu"il n'est soumis qu'à son poids
ici F n'est pas le poids, c'est une force constante: F = F j (avec j vecteur directeur de (Oy)
Oui je l'ai écrite, comme nous n'avons qu'une seule force j'ai donc F=ma et j'ai écris a=F/m
Ensuite pour les équations horaires j'ai écris :
ax(t)=0 ( car F est dans la direction de 0x ) et ay(t)=a ( positif du coup non ? )
puis j'ai intégré tel que vx(t)=v0x et vy(y)=at+v0y
Enfin x(t)=v0xt+x0 et y(t)=1/2at²+v0yt+y0
pour trouver la trajectoire j'ai fait t=x-x0/v0x et remplacé dans y, mais x0=0 ? Je ne sais pas trop ça me semble laborieux.... Je pense que quelque chose est encore obscurcie pour pouvoir me débloquer.
F n'est pas forcément positif
donc F=ma et j'ai écris a=F/m
attention F = m a est une relation vectorielle
ici dans (O,x,y) F (0, F) et a (ax, ay) donc
m ax = 0 et m ay = F
ce qui donne bien: ax=0 et ay = F/m
après intégration on trouve effectivement:
x(t)=v0xt+x0
y(t)=1/2 F/m t²+v0yt+y0
ce sont des équations générales et il faut tenir compte des conditions initiales du mouvement avant de continuer:
ici, à t=0: Vox = ... Voy = ... xo = ... yo = ...
" m rentre dans la région grisée avec une vitesse V0 ( selon l'axe Ox ) "
Donc pour les conditions initiales à t=0 on a :
V0x= V0 V0y=0 x0=0 y0=0 ?
ce qui donne t=x/V0
et y(t)=1/2*F/m*(x/V0)² ?
oui, la trajectoire est une branche de parabole
mais on note une trajectoire: y = f(x) et non pas y(t) = f(x) (car on élimine le temps des équations horaires)
D'accord, j'ai compris, merci.
Mais pour x=L nous avons juste a remplacer x par L dans l'équation de la trajectoire ?
Donc y1=(1/2)*(F/m)*(L²/V0²), c'est cela ?
Pour (ii) Pour la trajectoire dans la région 2, j'arrive à :
x(t)=V0xt+x0
y(t)=v0yt+y0
Mais V0y=0 ... y(t)=0 ? Trajectoire nulle ? La particule stagne ?
(ii) Déterminer la trajectoire de la particule dans la région II lorsque la particule est sortie de la région I. Commentez la trajectoire obtenue.
x(t)=V0xt+x0
y(t)=v0yt+y0
oui, effectivement dans la zone II la particule est isolé donc l'accélération est nulle (mouvement rectiligne uniforme)
mais attention aux conditions initiales: ce mouvement est un nouveau mouvement, il commence en x=L donc la position initiale et la vitesse initiale sont:
xo = L
yo = ...
vitesse en x=L du mouvement dans la zone I (notée V1 sur mon dessin)
Vox = ..
Voy = ..
D'accord, mais du coup y0=0 ?
Pour les vitesses je dois poser sin et cos ? Je suis complètement embrouillée là...
le mouvement dans la zone 1 a pour éq. hor. :
x(t)=vo t
y(t)=1/2 F/m t²
et la vitesse vaut
Vx(t) = Vo
Vy(t) = F/m t
donc quand x=L, y=y1=(1/2)*(F/m)*(L²/V0²), et t = x/Vo = L/Vo
donc en x=L, V1x = Vo
V1y = F/m.L/Vo = FL/(mVo)
x=L; y=y1 est la position initiale du second mouvement dans la zone II
et V1 (V1x,v1y) est la vitesse initiale du second mouvement dans la zone II
Ok, donc je trouve y=(FL/mV0)*((x-L)/V0)+y1 et y1 que je remplace avec ce que j'avais trouvé auparavant, je peux factoriser par FL/mV0 :
y=(FL/mV0)*((x-L/V0)+(L/2V0))=(FL/mV0)*(2x-L/2V0)
Mais, comment commenter cette trajectoire ?

 F = m a
F = m a
