Inscription / Connexion Nouveau Sujet
loi du mouvement de newton
Bonsoir.de laide svp
Un solide de masse M=0,4kg quitte le sommet dune piste avec une initiale nulle et glisse vers le bas..Sa position est a chaque fois repérer par l'angle 
Montrer par deux methodes différente que le solide quittera la piste avant d'atteindre le sol
Merci d'avance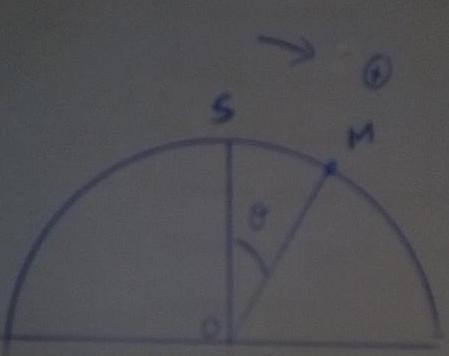
***Image recadrée***
Les frottement sont negligeable.
1ere methode:J'ai utilisé le théorème de l'énergie cinétique et le théorème du centre d'inertie et la base de frenet j'ai trouvé l'expression de la réaction R en fonction de m, g et  et quand je pose égale à 0 je trouve un angle inférieur à 90° donc il quitte la gouttière avant le sol
et quand je pose égale à 0 je trouve un angle inférieur à 90° donc il quitte la gouttière avant le sol
Maintenant pour la deuxième méthode je sais pas comment faire
Hello
Tu n'es pas disert en ce qui concerne ton raisonnement et ses étapes ... Je ne le serai pas plus 
1ere méthode: RFD
2eme méthode: Th de conservation de l'énergie mécanique
Dans les 2 cas le point décolle pour cos = 2/3
= 2/3
PS: refais l'exercice avec une vitesse initiale v0 
Hello
L'énergie mécanique du solide ce conserve, le travail de la réaction du support étant nul en l'absence de frottements:
Donc
soit (vitesse initiale nulle)
donc
Or la RFD nous dit (en projetant sur l'axe OM)
Cette deuxième méthode, comparée à la première qui n'utilise que la RFD, "t'économise" une dérivation pour résoudre le système de 2 équations issu des projections sur les 2 axes
Ce qui conduit à
Je comprends ton raisonnement pour la méthode 2.mais comment l'utiliser pour montrer que ça quitte avant d'atteindre le sol
Lorsque 3cos -2 = 0 (soit donc cos
-2 = 0 (soit donc cos = 2/3, soit
= 2/3, soit  = 48,...°) , R devient nulle: il y a donc décollement du support sphérique!
= 48,...°) , R devient nulle: il y a donc décollement du support sphérique!
Mais tu me diras, ce n'est pas parce qu'en un point du parcours R= 0 , que l'on a prouvé que le solide quittait "définitivement" la sphère ...
(ce dont se contentent la plupart des corrigés de ce pbm)
Je te réfléchir à une solution prouvant que R reste nulle ...
Tu me rends plus curieux encore ..donc si la reaction est nul le solide ne quitte pas forcément la piste ?
Si la réaction est nulle, le solide n'est plus en contact avec la piste.
Nous avons donc prouvé qu'en 
 48°, le solide n'était plus en contact avec le support.
48°, le solide n'était plus en contact avec le support.
il n'est peut être pas inutile de ne pas s'arrêter à R = 0 en 
 48°, donc le solide "décolle", mais de préciser que dans la suite de sa chute (devenue chute libre) il s'éloigne de la sphère
48°, donc le solide "décolle", mais de préciser que dans la suite de sa chute (devenue chute libre) il s'éloigne de la sphère 
Je comprends ce que tu dis mais le professeur dit d'utiliser une méthode dans laquelle on calcule pas l'angle ou la réaction est nul...
hum hum, c'est à ton tour (à celui de ton prof) de me rendre curieux.
La relation fondamentale de la dynamique et le Th de l'énergie mécanique me semblaient 2 candidats "désignés" ...
Une méthode qui ne passe pas par l'expression de l'annulation de la réaction du support (avec détermination explicite de l'angle limite ou pas) me laisse assez perplexe:
1) je vais continuer à réfléchir à te proposer une solution satisfaisante
2) je place un  car je sais qu'il y a sur ce site des bien plus "sachants" que moi en mécanique newtonienne
car je sais qu'il y a sur ce site des bien plus "sachants" que moi en mécanique newtonienne
3) Si dans l'intervalle tu obtiens un corrigé, n'hésite pas à partager, cela me semblerait intéressant
D'accord Mr Dirac...donc si je comprends bien il peut perdre contact avec la piste et reprendre contact un instant a l'autre
Pas tout à fait!
Ce que je voulais dire c'est qu'en une certaine position, le réaction R devenait nulle (la valeur de theta dont le cosinus vaut 2/3).
Donc en ce point le mobile "décolle" et entame une "chute libre".
D'un point de vue "physique", jusqu'à la valeur limite de theta la sphère contrarie la chute libre en imposant une poussée (la réaction du support) vers le "haut" qui fait que la trajectoire est circulaire et non pas parabolique (la trajectoire de la chute libre):
et ceci parce que jusqu'à cette valeur limite, le rayon du cercle est supérieur à ce que serait le rayon de courbure de la parabole de la chute libre.
Par contre, arrivé en cette position limite, le rayon de courbure de la parabole de la chute libre devient plus important que le rayon de la sphère, le mobile peut décoller et poursuivre suivre sa chute ... librement 
Dans les deux c'est le théorème de l'énergie mécanique ont utilise plus RFD...je vois pas la difference
Bon, j'ai continué à réfléchir comme annoncé. Voila ce que je peux te proposer comme "seconde" méthode qui prouve que le mobile décolle passer par le calcul de la réaction et la détermination d'un angle limite
Rappel des épisodes précédents:
dans le repère de Binet du mobile, le mouvement circulaire du mobile se décrit par:
Soit
Faisons l'hypothèse que le mobile reste en contact avec la sphère lorsque  varie de 0 à
varie de 0 à  /2
/2
sin varie de 0 à 1, donc la vitesse est croissante d'après (2) (ouf, cela semblait évident!)
varie de 0 à 1, donc la vitesse est croissante d'après (2) (ouf, cela semblait évident!)
Donc est positif croissant avec le temps,
Or mgcos varie de mg à 0
varie de mg à 0
Et -R est négatif ou nul
Donc l'équation (1) ne peut être vérifiée sur l'ensemble de l'intervalle [0 ,  /2]
/2]
Pourtant cette équation est dictée par la relation fondamentale de la dynamique (donc c'est du sérieux!)
Cela veut dire que l'hypothèse faite est fausse. Et si elle est fausse sa négation est vraie: le mobile décolle
Dans les deux c'est le théorème de l'énergie mécanique ont utilise plus RFD...je vois pas la difference
Pas tout à fait, comme je te le disais précédemment
Dans un cas on utilisait que la RFD et on passe par une étape de calcul de dérivée pour résoudre le système de 2 équations données par la RFD projetée
Dans l'autre cas, on utilise que l'une des équations et on remplace l'autre par le théorème de l'énergie cinétique (ou mécanique)
La différence n'est pas énorme me diras tu mais tu voulais 2 méthodes ... te voilà maintenant avec 3 ...
Pas de souci. Il est tjrs intéressant de chercher des manières différentes de regarder un même problème (même si en fait ici, l'objet est toujours d'étudier R)
D'ailleurs je m'aperçois que j'ai plus haut noté R 1) et le rayon de la sphère 2) et la réaction du support, mais tu auras fait je n'en doute pas la part des choses.
Si une autre méthode émerge de la correction du pbm en classe, n'hésite pas à partager ici 


