Inscription / Connexion Nouveau Sujet
loi de laplace
Bonjour
Enonce:
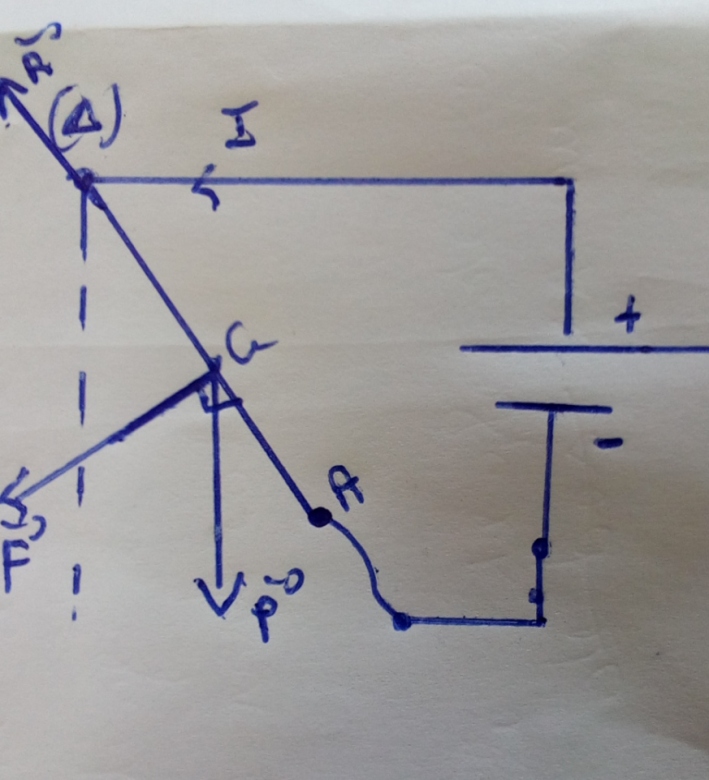
Au secours d une seance de travaux pratiques ,le professeur demande a ton groupe de determiner l intensite I du courant qui traverse un conducteur placé dans un champ magnétique uniforme B. Le dispositif utilisé est schématisé ci dessous .
Le conducteur rectiligne rectiligne OA ,homogène ,de masse m et de longueur l est susceptible de tourner dans un plan vertical autour d un axe horizontal (?) passant par son extrémité O . l autre extrémité est reliée a un fil conducteur souple qui permet de maintenir le contact électrique avec un générateur de tension continue. Le champ magnétique est horizontal et orthogonal au plan de la figure
Tu es le rapporteur du groupe
1/ décris ce que tu observes lorsque le circuit est ouvert
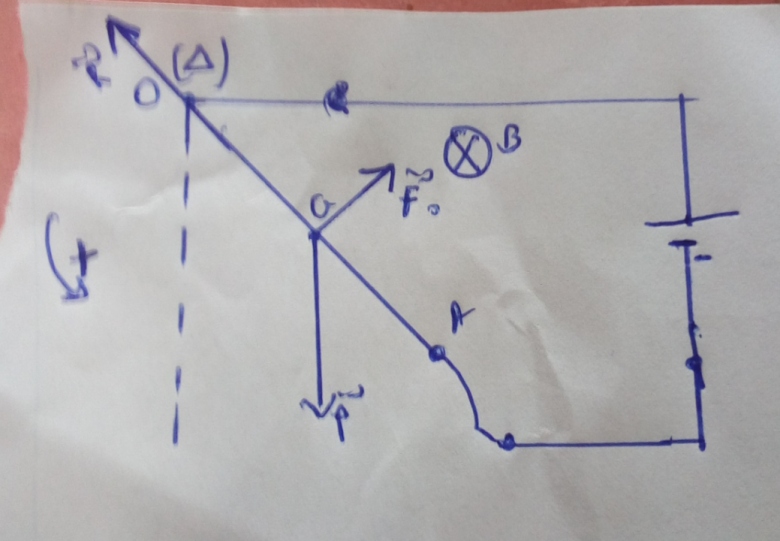
2. Représente sur un schéma les forces agissant sur le conducteur lorsque le circuit est fermé
3/ écris la condition d équilibre du conducteur susceptible de tourner autour de l axe (?) horizontal passant par son extrémité O
4/ détermination de l intensité I
4/1 . déduis de la question 3 l expression de l intensité I du courant qui traverse le conducteur
4/2 calcule la valeur de m intensité
Donnees
m=20 g, l=10 cm , B=0,5 T
a=30° , g=10 m/s
Bonsoir
Question 1
La tige (OA) se déplace et perpendiculaire a (B), lorsqu on fait circuler un courant intense dans ceux ci
Lorsqu on inverse le sens du courant ,le centre du mouvement change .
Lorsqu on supprime I ou B il n y a pas plus déplacement de ma tige.
Question 2
J aimerais savoir pour la présentation
Je dois représenter[quote]e] ses forces points O ou A
Bonjour
Tu peux appeler G le centre d'inertie de la tige homogène OA.
Quelles sont les forces appliquées à la tige OA ? Tu connais la loi de Laplace je suppose. Tu peux représenter les vecteurs forces sur le schéma et le poster ici.
Pour obtenir la condition d'équilibre qui permet de calculer l'intensité I, le plus simple consiste à considérer que la somme des moments des forces appliquées à la tige, par rapport à l'axe de rotation passant par O, est nulle.
Je te laisse travailler...
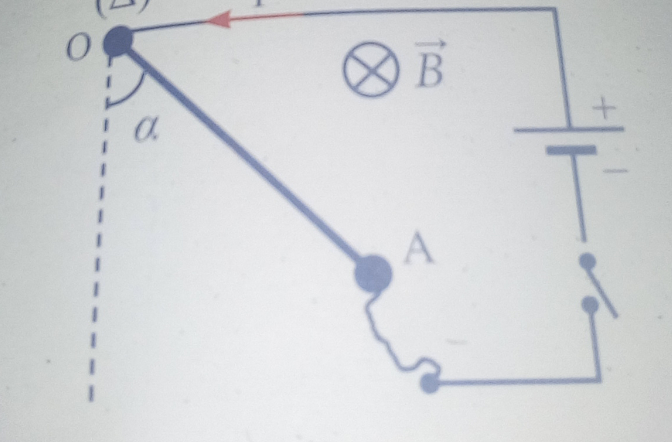
D'accord avec les points d'application des trois forces. Sinon le sens de la force de Laplace n'est pas réaliste. Par rapport à la position verticale obtenue en absence de courant, la tige tourne dans le sens anti horaire. La cause de cette rotation est la force de Laplace. Telle que tu l'as représentée, cette force aurait entraîné une rotation en sens inverse.
Corrige le sens de la force de Laplace puis applique le théorème des moments en prenant comme sens positif de rotation celui que tu veux. Cela ne va pas influencer le résultat.
Question 3
M(P)+M(F)+M(R)=0
Question 4/1
-P*l/2+F*l/2=0
P*l/2=F*l/2
P=F
mg=i*l*B
i=(mg)/lB
Question 4/2
I=(0,002*10)/0,1*0,5
I=0,4 A
Voilà qui est mieux ! Juste un détail : il n'est pas certain que la direction de la réaction R soit celle de la tige. La réaction R va juste compenser la somme vectorielle ) et comme tu ne connais pas encore
, impossible de déterminer avec précision la direction de
.
Pas grave car le moment de par rapport à l'axe de rotation est nul.
Attention : le moment du poids fait intervenir l'angle de rotation. Revois bien ton cours sur les moments de force par rapport à un axe.
Question 4/1
-P*GH+F*l/2=0
OHB est un triangle rectangle en H
Sin a=GH/OG
GH=sina*l/2
-P*sin a*l/2+F*l/2=0
Psina =F
m*g*sin a=i*l*B
i=(m*g*sina)/l*B
Question 4/2
i=(0,002*10*sin30°)/0,1*0,5
i=0,2 A
Étourderie sans doute : m=20g=0,020kg ; cela conduit à une intensité de 2,0A et non de 0,20A.
Sinon, comme déjà dit, la réaction R n'est pas nécessairement dans le prolongement de la tige OA dans le cas général.
Cependant, nous sommes ici dans le cas particulier de la statique puisque la tige est en équilibre. Dans ce cas particulier, le vecteur R a bien la direction de la tige. En effet, en statique, les lignes d'actions des trois forces sont concourantes.
Lorsque le circuit est ouvert, l'absence de courant annule la force de Laplace. La tige OA reste verticale :  = 0.
= 0.
Circuit ouvert F=0 car I=0 ;  =0.
=0.
Circuit fermé F>0 car I>0 ; c'est l'étude faite aux questions 2 et suivantes.