Inscription / Connexion Nouveau Sujet
les oscillateurs et la mesure du temps
J'ai un exercice sur les oscillateurs et la mesure du temps, je n'y arrive pas du tout, j'aimerais avoir de l'aide svp.
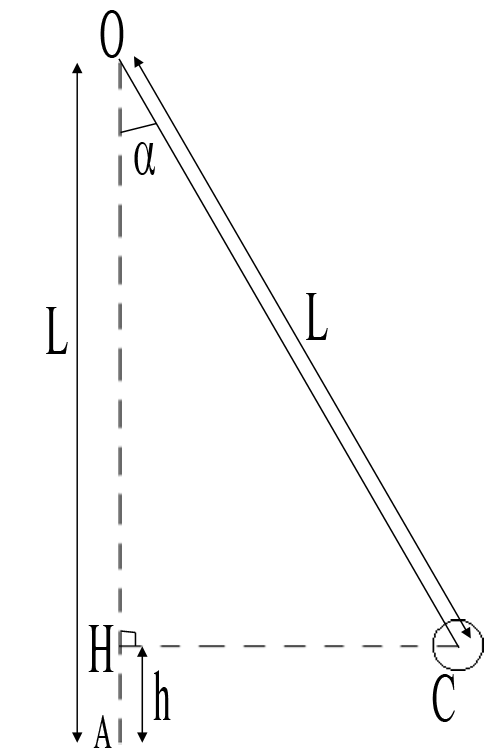
La sujet : Une horloge à "poids" s'arrête de fonctionner si l'on ne remonte pas son "poids". Le balancier d'une telle horloge à "poids" peut etre modélisé par un pendule formé d'un fil de longueur L= 1.0m et d'un point matériel de masse m=0.85kg. Le balancier bat la seconde : sa période est T=2.0s. Les oscillations sont entretenues par la très lente descente, d'une hauteur maximale de H=1.2m, du "poids", c'est a dire d'un cylindre de masse M=8.0kg.
Etudions pourquoi une telle horloge s'arrete et quel est le role du cylindre pour son fonctionnement.
1. Lorsque le pendule fait un angle ¤ avec la verticale, établir que l'altitude h du point matériel par rapport a sa position d'équilibre est h=L(1-cos¤)
2. Si le cylindre n'a pas été remonté, l'amplitude des oscillations passe de 6° à 5° après 15 oscillations du pendule :
- Calculer la variation moyenne de l'énergie mécanique du pendule pour une oscillation.
-Proposer une interprétation pour cette variation.
3. Lorsque le cylindre est remonté, il compense intégralement en descendant la variation d'énergie mécanique du pendule. Quelle est l'énergie moyenne transférée au pendule a chaque oscillation? de quelle hauteur est alors descendu le cylindre ? quelle est l'autonomie de l'horloge ?
Je n'y arrie vraiment pas, c'est notée en plus --' ..
Pour la 2
A l'élongation maximale, l'énergie mécanique est égale à l'énergie potentielle (puisque Ec = 0).
Il suffit donc de calculer l'énergie potentielle pour un angle de 6° et pour un angle de 5°.
Ensuite, pour trouver la variation moyenne pour une oscillation, il suffit de diviser la différence par 15.
Lorsque le cylindre est remonté, il compense intégralement en descendant la variation d'énergie mécanique du pendule. Quelle est l'énergie moyenne transférée au pendule a chaque oscillation ?
Donc l'énergie moyenne transférée au pendule à chaque oscillation est égale à la valeur que tu as trouvée à la question 2.
De quelle hauteur est alors descendu le cylindre ?
L'énergie moyenne transférée au pendule à chaque oscillation est égale à la variation d'énergie potentielle du poids c'est-à-dire mgh avec m = masse du pendule, g = accélération de la pesanteur, h = hauteur dont le poids est descendu.
Quelle est l'autonomie de l'horloge ?
Le résultat est en oscillations du pendule !
Donc il faut multiplier par 2 s pour trouver le temps (en secondes).
Il faut, selon le résultat, transformer le temps en heures et même sans doute en jours...
Je vous remercie beaucoup de votre aide. Jai pu comprendre un peu. La mécanique en physique cest vraiment pas mon truc ^^
up ! Concernant cet exercice si quelqu'un pourrait m'expliquez comment on répond a la question par quels calculs ou autres je ne comprends pas :/
je me suis mal exprimée desolé, par rapport a la question a j'ai compris comment résoudre d'ailleurs la reponse se trouve dans le topic mais donc par rapport a la suite de cet exercice a la question b, voir c . Je n'arrive pas a calculez la variations moyenne de l'energie mecanique, selon moi il faut faire :
Em(6 degré) - Em(5 degré) pour avoir la variation moyenne.
Cependant il faut donc calculer l'energie potentielle et cinetique de ces des energies mecanique et je 'arrive pas a toruver la vitesse v par exemple;
Je suis vraiment fatigués cela fait une semaine que je n'avance pas, donc si l'on pourrait m'expliquer voir me donner les reponses pour que je puisse refaire apr moi même et me corriger sa serait geniale !
Lorsque le pendule est à l'élongation maximale, l'énergie cinétique est nulle. L'énergie mécanique ets donc égale à l'énergie potentielle.
Pour 6°:
Ep1 = m g h = m g L(1-cos(6°))
Pour 5°:
Ep2 = m g h = m g L(1-cos(5°))
Donc, sur 15 oscillations :
Pour 1 oscillation :
interprétation de la variation ==> perte d'énergie avec les frottements
Lorsque le pendule descend de h, son énergie potentielle diminue de m g h. Cette énergie est transmise au pendule.
Donc :
Autonomie de l'horloge
Pour 1 oscillation, le poids descend de h. Il peut descendre de H = 1,20 m.
Nombre d'oscillations :
Comme une oscillation dure 2 secondes, l'autonomie de l'horloge sera :
Erreur !...
Lorsque le pendule descend de h, son énergie potentielle diminue de m g h. Cette énergie est transmise au pendule.
Donc :
Correction
Lorsque le pendule descend de h, son énergie potentielle diminue de m g h. Cette énergie est transmise au pendule.
Donc :
J'ai oublié un bout...
Donc :
Donc :
soit
Nombre d'oscillations :
Comme une oscillation dure 2 secondes, l'autonomie de l'horloge sera :
soit environ 2 jours 8 heures 9 minutes 5 secondes
Merci beaucoup, juste une derniere question.
Pouvez-vous expliquer pourquoi on ne parle pas d'energie cinetique , quad le pendule est a 5 degrés il acquiert une vitesse ? qui influe donc sur l'energie mecanique ?
Quand le pendule est à 5°, il acquiert une vitesse... C'est exact mais à quel endroit ?...
L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle. A la verticale, l'énergie cinétique est maximale et l'énergie potentielle est nulle. A l'élongation maximale, l'énergie potentielle est maximale (la plus grande hauteur) et l'énergie cinétique est nulle (vitesse = 0). Mais la somme est constante quand il n'y a pas de frottement (perte d'énergie) (frottement ou ici, entraînement du mécanisme de l'horloge qui peut être assimilé à un frottement et, en tout cas, à une perte d'énergie).
Donc, quand le pendule est à l'élongation maximale, l'énergie potentielle est maximale et l'énergie cinétique est nulle. En ce point, l'énergie mécanique est égale à l'énergie potentielle (l'énergie cinétique étant nulle).


 ) ?
) ?
 Je vais éssayer de faire la suite mais cest pas gagné
Je vais éssayer de faire la suite mais cest pas gagné
