Inscription / Connexion Nouveau Sujet
Les grandeurs cinématiques du mouvement
Bonsoir, j'ai du mal avec un exercice et je demande votre aide.
Exercice:
Les équations paramétriques du mouvement d'un mobile se déplaçant dans le repère orthonormé (O;i;j) sont:
OMvecteur
x=Rcos( t+
t+ )
)
y=Rsin( t+
t+ )
)
Où  =2
=2 rad.s-1 et R=8cm.
rad.s-1 et R=8cm.
1. Déterminer  sachant qu'à t=0, M a pour coordonnées x0=0 et y0=R.
sachant qu'à t=0, M a pour coordonnées x0=0 et y0=R.
2. Établir l'équition de la trajectoire de M. Quelle est sa nature ?
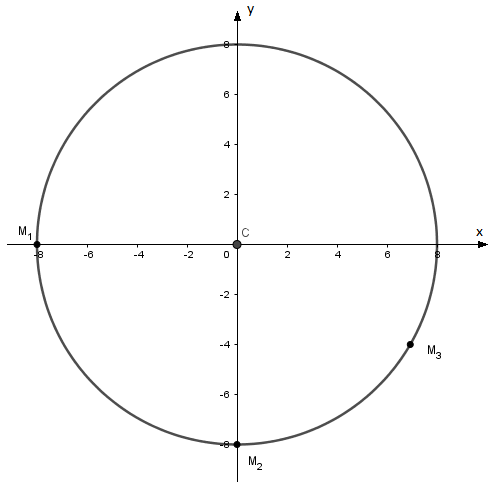
3. Représenter cette trajectoire dans le repère (O;i;j). Échelle: 1cm=2cm.
4. Montrer que la vitesse linéaire de M est constante. Faire l'application numérique.
5. Montrer que l'accélération linéaire de M est constante. Faire l'application numérique.
6. Représenter sur la trajectoire, les points M1, M2 et M3 du mobile M respectivement aux instant t1=0,25s, t2=0,5s et t3=2/3s
Ma solution:
1. Déterminons 
 =cos-1(0)=
=cos-1(0)= /2
/2
 =sin-1(0)=0
=sin-1(0)=0
2. Équation de la trajectoire
x2+y2=R2
x2+y2=0,64
Nature: La trajectoire est un cercle de centre O(0;0) et de rayon 0,08 m.
6. Position de M1
x=-4 2
2
y=4 2
2
Position de M2
x=-8
y=0
Position de M3
x=-4 3
3
y=-4
Je ne parviens pas à représenter ces points sur la trajectoire car je ne sais pas comment tracer la trajectoire dans le repère orthonormé (O;i;j).
Je n'arrive pas non plus à démontrer que la vitesse linéaire de M et son accélération linéaire sont constantes.
Je vous prie de m'aider et de corriger mes erreurs au cas où j'en aurai faites.
Re - bonjour !
Question 1:
OK
Question 2:
En cm : x²+y² = R² = 64
En m : x²+y² = R² = 0,08² = 6,4.10-3
Questions 4 et 5 :
A partir des expressions de x(t) et y(t) calculer vx(t) , vy(t) , v(t)
Même démarche pour l'accélération
Question 6 :
Je ne trouve pas les mêmes résultats que toi, mais comme tu ne détailles pas tes calculs, impossible d'en savoir plus.
Je ne parviens pas à représenter ces points sur la trajectoire car je ne sais pas comment tracer la trajectoire dans le repère orthonormé (O;i;j).
Je te conseille d'utiliser un instrument, devenu un peu "ringard" mais qui a fait ses preuves. Cela s'appelle un compas !
Merci pour votre aide.
Pour les questions 4 et 5, lorsque je calcule Vx, j'obtiens -Rsin( t+
t+ ) et quand je calcule Vy, j'obtiens Rcos(
) et quand je calcule Vy, j'obtiens Rcos( t+
t+ ). Si mes calculs sont corrects, en quoi cela démontre-t-il que la vitesse est constante ?
). Si mes calculs sont corrects, en quoi cela démontre-t-il que la vitesse est constante ?
Pour le calcul de l'accélération je trouve ax=-Rcos( t+
t+ ) et ay=-Rsin(
) et ay=-Rsin( t+
t+ ).
).
Ensuite pour expliciter mes calculs à la question 6.
M1:
x=8cos(2 (1/4)+
(1/4)+ /2)=-8
/2)=-8
y=8sin(2 (1/4)+
(1/4)+ /2)=0
/2)=0
M2
x=8cos(2 (1/2)+
(1/2)+ /2)=0
/2)=0
y=8sin(2 (1/2)+
(1/2)+ /2)=-8
/2)=-8
M3
x=8cos(2 (2/3)+
(2/3)+ /3)=4
/3)=4 3
3
y=8sin(2 (2/3)+
(2/3)+ /2)=-4
/2)=-4
Aidez-moi et dites-moi si je me trompe, s'il vous plaît.
Question 4:
Il te faut revoir tes cours de mathématiques sur la dérivation:
x(t) = R * cos( t +
t +  ) donne par dérivation :
) donne par dérivation :
Vx(t) = - R *  * sin(
* sin( t +
t +  )
)
Exprime Vy(t) à partir de y(t) , puis exprime V en te servant de V² = (Vx)² + (Vy)²
Tu devrais alors constater que V ne dépend pas de t et donc que V est constant.
Question 5:
Même procédé que pour la question 4
On exprime ax(t) et ay(t) en dérivant Vx(t) et Vy(t) puis on utilise a² = (ax)² + (ay)² pour obtenir a
Question 6 :
Cette fois, tu trouves la même chose que moi.