Inscription / Connexion Nouveau Sujet
Les grandeurs cinématiques du mouvement
Bonsoir, j'ai du mal à répondre à des questions de mon exercice, je vous prie de m'aider et de corriger mes erreurs au cas où j'en aurai faites.
Exercice:
Dans un repère (O;i;j), orthonormé, les lois horaires du mouvement d'un mobile ponctuel M sont données par: x(t)=t et y(t)=t2/2, le temps est mesuré en seconde et les distances en m.
À t=0 s, le mobile débute son mouvement.
1.
a) Quel est le point de départ du mobile à l'origine des dates ?
b) Établir l'équation de la trajectoire du mobile relativement au repère (O;i;j).
c) Déterminer l'expression du vecteur vitesse et celle du vecteur accélération du mobile M.
2.
a) À quelle date le vecteur vitesse est colinéaire à i (vecteur) ?
b) Montrer qu'à cette date la composante tangentielle de l'accélération est nuelle.
3. Sachant qu'à une date t l'accélération tangentielle a pour expression at=t/[V(1+t2)] dans le repère de Frénet (M,t,n). Montrer que celle de l'accélération normale an=1/[V(1+t2)].
4. À quelle date t1, Vx=Vy avec Vx et Vy les composantes du vecteur vitesse V (vecteur) dans le repère (O;i;j) ? Calculer le rayon de courbure de la date t1.
Ma solution:
1.
a) Soit M0 le point de départ du mobile M. Le point de départ du mobile est M est:
M0=0
b) Déterminons l'équation de la trajectoire de M.
y=x2/2 : la trajectoire est une parabole.
c) Déterminons l'expression du vecteur vitesse:
Vvecteur=ivecteur+tjvecteur.
-Déterminons l'expression du vecteur accélération.
avecteur=jvecteur.
2.
a)Trouvons la date à laquelle le vecteur vitesse est colinéaire au vecteur i.
Le vecteur vitesse est colinéaire au vecteur i s'il existe un réel k tel que V(vecteur)=ki(vecteur).
La date à laquelle V(vecteur) est colinéaire à i(vecteur) est t=0 s car à cette date: V(vecteur)=i(vecteur).
D'où t=0 s.
b) Montrons qu'à cette date la composante tangentielle de l'accélération est nulle.
-Calculons le module de la vitesse:
V=1 m.s-1.
at=0 (car V est une constante).
Je n'arrive pas à résoudre le reste, aidez-moi, s'il vous plaît.
Je m'excuse pour le manque de détails au niveau de mes réponses mais ce message étant déjà très long, une fois détaillé il prendrait plus de temps à être écrit.
Légende:
"V" est mis pour la racine carré.
Bonjour,
Question 1a)
Je pense que la réponse attendue concerne les coordonnées de M0
Questions 1b), 1c), 2a)
OK
Question 2b)
Le fait qu'à la date t=0, la vitesse soit égale à 1 ne prouve nullement que l'accélération tangentielle soit nulle.
Quelle propriété possèdent à la date t=0 le repère cartésien et le repère de Frenet ?
Conclusion ?
Tout d'abord merci pour votre aide.
Ensuite, au sujet du calcul de la vitesse, je voulais préciser qu'il n'est pas présent pour démontrer que la composante tangentielle de l'accélération est nulle mais il est là pour me permettre de calculer l'accélération tangentielle car voulant utiliser la formule at=dV/dt (avec dV la dérivée de la vitesse), j'ai nécessairement besoin de la valeur de la vitesse. Puis dérivant cette valeur qui est une constante, le résultat obtenu est 0.
Hormis ça, je ne parviens toujours pas à répondre aux questions 3 et 4 de l'exercice, sur ce, je vous demande encore de l'aide.
b) Montrons qu'à cette date la composante tangentielle de l'accélération est nulle.
-Calculons le module de la vitesse:
V=1 m.s-1.
at=0 (car V est une constante).
Avoir trouvé la valeur de la vitesse à la date t=0 ne montre pas que la vitesse constante !
En fait ce mouvement n'est pas un mouvement uniforme.
La vitesse n'est pas constante.
Question 3 : Il suffit d'appliquer la relation a² = (at)² +( an)²
Question 4 :
Après avoir trouvé la date t1 à laquelle vx = vy utiliser à cette date t1 la relation an = v² /

Merci pour ces éclaircissements sauf qu'en ce qui concerne la question 2b, la seule idée que j'avais en tête était de calculer d'abord la vitesse puis la dérivée de cette dernière sauf que ce fait étant faux, je me retrouve sans moyen de démontrer que la composante tangentielle de l'accélération est nulle. J'ai besoin d'aide là dessus.
Ensuite en ce qui concerne la question 3, j'ai essayé de tirer an de la formule a2=(at)2+(an)2 mais je ne parviens pas à retrouver l'expression at=1/[V(1+t2)]
Voici comment je procède
a2=(at)2+(an)2
(an)2=a2-(at)2
(an)2=(1)2-t/[V(1+t2)]
(an)2=[V(1+t2)-t]/[V(1+t2)].
À partir d'ici je bloque, aidez-moi à avancer ou mettez-moi sur le chemin de la justesse.
Enfin, en ce qui concerne la question 4, je ne vois pas comment déterminer t1.
S'il vous plaît, aidez-moi encore.
Légende:
"V" est mis pour la racine carré.
je me retrouve sans moyen de démontrer que la composante tangentielle de l'accélération est nulle. J'ai besoin d'aide là dessus.
L'aide que tu réclames, je te l'ai déjà apportée dans mon post du 28-09-19 à 08:47
Question 3 :
Revois ton calcul.
L'énoncé indique :
donc
Merci encore pour vos explications, j'ai pu achever la démonstration de l'expression an de la manière suivante:
an2=1-[t2/(1+t2)]
an2=(t2+1-t2)/(t2+1)
an2=1/(t2+1)
an=1/[V(t2+1)].
Par contre, je ne connais pas la propriété à la date t=0 que possèdent le repère cartésien et le repère de Frénet. Quelle est-elle ?
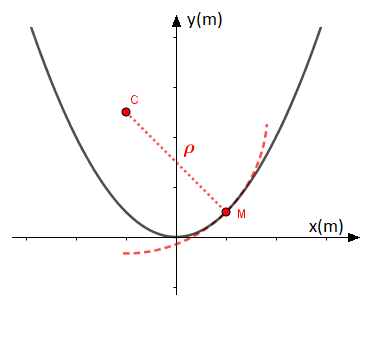
Il faut dessiner la courbe représentative de la trajectoire du mobile pour se rendre compte qu'à la date t=0, le mobile se trouve en M0 ( 0,0 ) et qu'à cet instant là ( et seulement à cet instant là ) le repère (fixe) O,i,j et le repère (mobile) de Frenet sont superposés.
Cela signifie qu'à cet instant là les vecteurs et
d'une part et les vecteurs
et
d'autre part sont égaux.
On a donc ( toujours à la date t=0 )
et
On en déduit que at = 0 ( et an = 1 )
Très simplement.
L'énoncé donne x(t) et y(t)
On en déduit Vx(t) et Vy(t)
et on recherche la date t=t1 pour laquelle Vx(t) = Vy(t)
J'ai une dernière inquiétude sur cet exercice.
J'ai pu déterminer t1=1. Maintenant, je dois déduire la valeur de R. Je suis parti de la formule an=V2/R D'où R=V2/an.
R=(V2)2/[1/V2]
R=2V2 m.
Est-ce correct ?
Légende:
"V" mis pour la racine carré.