Inscription / Connexion Nouveau Sujet
les gaz parfaits
l'équation d'état d'une mole de gaz appellé"gaz de Van der Waals" est : (P+a/V²)*(V-b)=R*T
calculer le travail qu'il faut fournir à n moles de ce gaz pour le faire passer d'un volume V1 à un volume V2 à la température constante T?
merci pour votre aide car la je ne vois pas par ou commencer
T est constante donc PV=P1V1+P2V2= CTE
T=(P1V1)/nR=(P2V2)/nR
n=(P1V1)/TR ou RT=P1V1/n
D'ou (P+a/V²)*(V-b)=P1V1/n
et apres????????????
Le travail W de la force de pression lors d'une transformation isotherme se calcule par la formule :
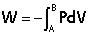
Il faut partir de la loi extensive de Van der Waals :
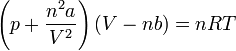
(puisque dans votre formule V, c'est le volume molaire Vm)
Exprimer P en fonction de (V, T et n)
Puis procéder à une intégration par rapport à V (sachant que T est une constante).
- il me semble -
je pensais dire que:
on passe de l'état(1) (P1,V1)--------------> l'état(2) (P2,V2)
la température au cours de la transformation étant constante on a : T=P1V1/nR=P2V2/nR= cte
le travail reçu du gaz :  W=-P.dV ---------> W12= -
W=-P.dV ---------> W12= - V1V2 P.dV
V1V2 P.dV
or W12=- V1V2 PV/V.dV
V1V2 PV/V.dV
W12=- V1V2 cte/V.dV
V1V2 cte/V.dV
W12=-cte V1V2 1/V.dV
V1V2 1/V.dV
W12=-cte[ln V]V1V2
W12=-P1V1 * (ln V2- ln V1)
W12=-P1V1* ln (V1/V2)
MERCI DE ME DIRE SI C EST JUSTE
Votre raisonnement et votre calcul sont corrects... A ceci près que vous êtes parti de l'équation des gaz parfaits au lieu de l'équation des gaz réels...
Donc votre  W est incorrect dès le départ...
W est incorrect dès le départ...
Comme je vous l'ai dit, on commence par exprimer P en fonction de V à partir de l'équation d'état de Van der Waals.
On va faire le raisonnement à partir de votre équation !
[imghttp://upload.wikimedia.org/math/e/e/d/eedc3552f11463e7e64caf5470d0b376.png][/img]
On transpose le terme (V-b)
<=> (P - a/V²) = RT/(V-b)
<=> P = RT/(V-b) - a/V²
On multiplie par la quantité dV
<=> P.dV = RT. dV/(V-b) - a.dV/V²
<=> -P.dV = -RT.dV/(V-b) + a.dV/V²
<=>  W = -RT.dV/(V-b) + a.dV/V²
W = -RT.dV/(V-b) + a.dV/V²
qu'il vous maintenant intégrer entre V1 et V2.
Effectivement, il y a une erreur dans mon équation de départ lors de la frappe :
Je reprends :
On a (P + a/V²) = RT/(V-b)
<=> P = RT/(V-b) - a/V² (là, j'ai bon ! Sûr !)
donc
W = -RT
 dV/(V-b) + a
dV/(V-b) + a
 dV/V2
dV/V2
(Vérifiez bien que quand vous avez fait passer +a/V² de l'autre côté, vous avez mis un signe - et qu'en multipliant par -dV, vous obtenez bien + a.dV/V²)
pardon j'avais repondu avant votre reponse
donc si je reprends
w= -RT*[ln(V-b)]V1V2 - a*[1/V²]V1V2
W= -RT*[ln(V2-b)-ln(V1-b)]- a (1/V2²-1/V1²)
je corrige
w= -RT*[ln(V-b)]V1V2 - a*[1/V]V1V2
W= -RT*[ln(V2-b)-ln(V1-b)]- a (1/V2-1/V1) = -RT*(ln(V2-b)-ln(V1-b)-a*(V1-V2)/V1V2


