Inscription / Connexion Nouveau Sujet
Les bases de la dynamique 3
Bonjour 
J'aurais besoin d'aide pour cet exercice. Merci de me guider
L'énoncé :
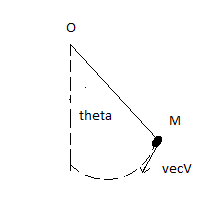
Une sphère (S) assimilable à un point matériel de masse = 50 g est reliée à un point fixe O par un fil inextensible de masse négligeable et de longueur l= 50cm.
Le fil est écarté de sa position d'équilibre 
0=π/3 rad,puis elle est lancée vers le bas avec un vecteur vitesse perpendiculaire au fil .A une date t quelconque ,la position de la bille est repérée par l'angle
que forme le fil avec la position d'équilibre .
1. Exprimer la vitesse V de la bille à la date t en fonction de V0, 1 ,g , 0 et .
2. Exprimer la tension T du fil à la date t en fonction de m ,V0,1,g ,0 et .
3. Quelle doit être la valeur minimale de V0 pour que la bille fasse un tour complet ,le fil restant rendu ?
Bonjour
Pense au théorème de l'énergie cinétique ou à la conservation de l'énergie mécanique.
Que proposes-tu comme solution ?
Étourderie je pense : Vo apparaît au carré dans la formule.
cos(o) doit intervenir dans l'expression... Mais tu y es presque !
J'allais oublier : compte tenu de l'expression de l'énergie cinétique, un "2" doit bien traîner quelque part...
Bonjour vanoise
Je m'étais trompé par la figure
Je reprends:
1)
mV2-mV02= 2mg(zf-zi)
V2= 2g (lcos-lcos0)-V02
Bonjour
Première ligne : OK sous réserve que l'axe (O,z) soit orienté vers le bas ;
Deuxième et troisième ligne : une étourderie j'espère concernant le signe devant Vo2.
Pour 2 : du premier coup d'œil, il est facile de constater que le résultat est erroné :
T a la dimension d'une force, comme le poids mg alors que v2/l a la dimension d'une accélération. Une force ne peut en aucun cas être égale à une accélération ! Il faut penser, pour chaque résultat littéral, à vérifier l'homogénéité ; cela permet d'éviter de grosses erreurs et de corriger de nombreuses étourderies. ÉVIDEMMENT, il faut éviter de mélanger dans une même formule valeur littérales et valeurs numériques car alors on perd tout moyen de vérification de cette homogénéité mais bon : je pense que tu sais cela ; il n'y a guère que les débutants qui commettent ce genre de faute de méthode ! 
Par exemple, l'expression suivante est homogène :
Pour 3), tel que je comprends la question, il faut trouver une condition sur Vo pour que le pendule effectue un tour complet à partir de la position initiale caractérisée par o=
/3rad. Il faut pour cela que le fil reste constamment tendu ; il faut donc : T>0 ; or la formule précédente montre que T est minimum pour cos()=-1...
Je te laisse corriger et terminer...
Tu n'avais donc pas compris mon message précédent...
T apparaît comme une somme de deux termes et T est une intensité de force. Il faut donc que chacun des deux termes de la somme ait la dimension physique d'une intensité de force. C'est le cas du terme en m.g, c'est le cas du terme en m.Vo2/l mais ce n'était pas le cas du terme en V2/l comme tu l'avais écrit...
Pour la dernière question, je t'avais pratiquement fournie la réponse...
Idem pour l'homogénéité de la réponse à 3) : la valeur limite de la vitesse doit nécessairement avoir la dimension d'une vitesse, ce qui n'est pas le cas de 
g. Si tu n'en es pas convaincu, intéresse-toi aux unités.
Cette remarque sur l'homogénéité valait aussi pour ta réponse d'hier à 12h45 :
Le carré d'une vitesse ne peut être comparé à un poids ! C'est un peu comme si tu disais que ta taille est supérieure à ton poids ! on ne peut comparer que des grandeurs de même nature ; on dit en physique : de même dimension.
Remarque : le théorème de l'énergie cinétique que tu as utilisé précédemment a montré que le carré d'une vitesse et le produit d'une accélération par une distance sont de même dimension physique. Il est donc possible de comparer Vo à ...
Parfait !
Au-delà de cet exercice, j'espère que tu as bien compris maintenant comment une simple vérification de l'homogénéité d'un résultat littéral permet d'éviter de grosses erreurs ou étourderies.
Annuler
connectez vous