Inscription / Connexion Nouveau Sujet
Le tir de précision
Bonjour j'ai un DM de physique a faire pour mercredi et je bloque sur certaines questions.
On considérera que le référentiel terrestre peut être assimilé a un référentiel galiléen, et on négligera les frottements dans l'air.
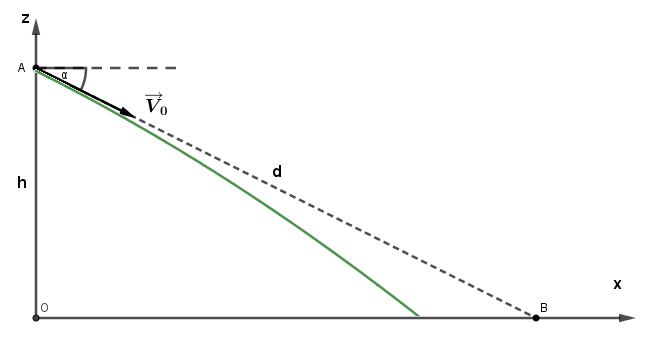
Un tireur d'élite est posté sur le toit d'un bâtiment de hauteur h. Il vise une cible se trouvant au niveau du sol à une distance d. Son fusil lance des projectiles de masse m, qui sortent du canon a une vitesse v0.
Le repère sera choisi de telle sorte que l'origine est au niveau du sol, a la meme abscisse que le tireur ( je ne vois pas comment le représenter). L'axe des abscisses (Ox) est orienté dans la direction du tir vers la cible ; l'axe des altitudes (Oz est orienté vers le haut.
On appelle  l'angle entre le vecteur vitesse initiale v0 et l'horizontale, comté positivement dans le sens trigonométrique. Ainsi,
l'angle entre le vecteur vitesse initiale v0 et l'horizontale, comté positivement dans le sens trigonométrique. Ainsi,  >0 correspond a un tir vers le haut et
>0 correspond a un tir vers le haut et  <0 à un tir vers le bas.
<0 à un tir vers le bas.
1)a. Exprimer les coordonnées du point de départ A de la balle , et celles de la cible B
b. Faire l'inventaire des forces s'exerçant sur la balle une fois sortie du canon du fusil, en déduire son accélération (vecteur) a
c. Déduire de tout cela les lois horaires du mouvement de la balle
d. Etablir l'équation de la trajectoire de la balle. De quelle nature est cette trajectoire ?
e. Faire un schéma où figureront les axes, A et B, l'angle  et y dessiner la trajectoire de la balle
et y dessiner la trajectoire de la balle
Voici le début de l'exercice et je bloque sur la question 1)a.
Les questions b. et c. sont faciles mais je bloque après sur la question d. et sur comment faire les schéma.
Merci d'avance pour ceux qui pourront m'aider
Lacryzz
Bonjour,
Je suppose que cette phrase :
" Il vise une cible se trouvant au niveau du sol à une distance d. "
signifie que le fusil est orienté selon la droite AB et donc que le vecteur vitesse initiale a aussi cette direction.
Dans ces conditions le projectile ne touchera pas le sol exactement au point B.
Voici la suite de l'exercice :
2) Pour atteindre sa cible, le tireur doit ajuster l'angle . On cherche à savoir comment il fait s'y prendre quand le fusil est munidune lunette de visée dont l'ace est parallèle à celui du canon.
. On cherche à savoir comment il fait s'y prendre quand le fusil est munidune lunette de visée dont l'ace est parallèle à celui du canon.
a. Déterminer l'angle  0 lorsque le tireur a sa cible exactement au centre du réticule (croix centrée dans le champ du viseur).
0 lorsque le tireur a sa cible exactement au centre du réticule (croix centrée dans le champ du viseur).
b. Déterminer les temps t1 que mettrait la balle pour aller du tireur à sa cible, en ligne droite, à la vitesse v0.
c. On suppose que le temps mis par la balle à atteindre la cible est pratiquement égal à t1
Calculer la déviation verticale  z0 de la balle par rapport à la ligne droite.
z0 de la balle par rapport à la ligne droite.
Si vous pouviez m'aider pour ces questions sachant que j'ai fait ceci pour les questions 1c. et 1d.
1)c.
On a après avoir dérivé :
vx = v0cos
vz = -gt + v0sin
On en déduit la loi horaire :
x = v0tcos
z = -1/2gt2 + v0sin
1)d.
On a : t =x/v0cos
d'où,
z = -1/2 gt2 + v0sin
et en remplaçant par t, on obtient :
z = -gx2/2v02cos2 + xtan
+ xtan
merci pour votre aide
lacryzz
La question 1.c est à revoir.
Et 1.d qui dépend de 1.c est à revoir également.
1)c.
vx = v0cos
 OK
OK
vz = -gt + v0sin
 OK
OK
On en déduit la loi horaire :
x = v0tcos
 OK
OK
z = -1/2gt2 + v0sin
 Non
Non
Effectivement pour z j'ai oublié le t en recopiant, on a :
z = -1/2 gt2 + v0tsin
Mais alors je ne vois pas ce qui est faux pour la 1d.
z = -1/2 gt2 + v0tsin

Tu as corrigé une des deux erreurs, il en reste donc une.
Indication :
Quelle est la valeur de z(0) d'après ton équation horaire ?
Quelle est la valeur de z(0) d'après l'énoncé ?
Conclusion ?
Il fait donc rajouter h à la fin
Mais donc j'écris que à t=0 on a z = 0. Ok j'ai compris merci.
Est ce que vous pourriez m'aider pour la question s'il vous plaît ?
Merci
Il fait donc rajouter h à la fin
Oui et l'équation horaire correctement écrite est donc :
z(t) = - (1/2) gt² + v0 sin(α) t + h
Question 2.a :
Il s'agit d'exprimer l'angle α0 en fonction de h et d
Rien de bien compliqué !
Question 2.a : Relation entre vitesse, distance parcourue et durée ....
J'ai commencé à dire que x=d donc on a :
v0 t cos alpha = d <=> t = d/ v0cos 
Mais après je sais pas s'il fait remplacer t dans z ou alors faire autre chose. J'avais pensé à écrire les lois horaires du mouvement de la cible pour ensuite écrire une égalité entre le z de la balle et le z de la cible et enfin trouver  en fonction de h et d.
en fonction de h et d.
Après avoir fait les calculs on obtiendrait z' (pour la cible) qui vaut : z' = -1/2gt2
Et donc on aurait z = z'
D'où on a aussi
t= -h/v0sin 
En égalisant les t on trouve : tan  = -h/d ce qui peut être assez logique car
= -h/d ce qui peut être assez logique car  est négatif étant donné que c'est un tir vers le bas.
est négatif étant donné que c'est un tir vers le bas.
Mais c'est peut être un peu compliqué
Question 2a)
J'ai commencé à dire que x=d .... etc
C'est mal parti !
x est l'abscisse du projectile, c'est une variable comprise entre x=0 et x= xB
d est une constante telle que d=AB ( distance qui sépare les points A et B
Donc aucune raison de dire que x=d !
Comme indiqué dans mon post du 24-03-19 à 17:51 il ne faut pas aller chercher bien loin.
Considère le triangle AOB et établis la relation entre α0 , h et d
C'est juste un peu de géométrie niveau classe de 3ème.
Dans le triangle OAB,
L'angle OAB =  /2 -
/2 -
cos OAB = h/d
Ce qui donne
sin = h/d
= h/d
Effectivement c'est très simple.
Pour la 2b.
On a v0 = d/t1
donc t1 = d/v0
Easy aussi merci.
Après je bloque sur la 2c.
Ce qui donne
sin
 = h/d
= h/d
Effectivement c'est très simple.
Attention tout de même !
"h" et "d" sont des constantes positives
α0 (l'énoncé impose α0 , tu ne peux pas nommer cet angle autrement !) est une constante négative donc sin(α0) est négatif aussi.
On aura donc : sin(α0) = - h/d
Pour la 2b.
On a v0 = d/t1
donc t1 = d/v0
On peut aller plus loin.
On vient de montrer que sin(α0) = - h/d ce qui équivaut à d = -h / sin(α0)
et par suite : t1 = d/v0 = -h / ( v0 sin(α0) )
Question 2c)
L'énoncé fait l'hypothèse que la durée de vol du projectile est approximativement égal à t1
Il te faut exprimer z(t1) et voir la différence obtenue par rapport au même temps de vol sur la trajectoire rectiligne AB
Mais le problème est que je trouve un angle négatif (je peux après l'ecrire en positif). On m'a donné comme valeur : h = 15.0 m
d= 200 m
v0 = 700 m.s-1
J'ai donc trouvé un angle de 4,3 degré mais ça me parait peu.
Après pour la 2b j'ai trouvé par moi même t1 = 286 ms et quand je fais votre méthode je trouve - 16 secondes 🧐 est ce normal ?
En calculant z(t1) je trouve 29,6 m
Et donc en calculant la position de B on trouve 199 m
Mais après comment je conclue ?
Mais j'ignore sur quelles questions on te demande des applications numériques.
J'ignore quel est l'angle de 4,3° dont tu parles.
J'ignore ce qu'est ce que tu nommes "ma méthode"
Bref, sans un minimum de rigueur je me redéclare incompétent.
En effet excuser moi.
On me demande une application numérique pour les questions 2a./b. et c.
Quand je parlais de ma méthode c'était pour la 2b. quand j'ai écris que t= d/v et j'ai trouvé un résultat différent que celui en passant par votre formule t= d/v sin
Question 2a)
On a trouvé :
sin(α0) = -h/d = -15/200 = -0,075
α0 = -4,30°
L'angle négatif correspond à un tir vers le bas (Voir l'énoncé à ce sujet)
Question 2b) :
t1 ( et non t !!!!) = d/v0 ( et non v!!!! ) = 200/700 = 0,286s = 286 ms
ou bien (voir mon post du 24-03-19 à 19:27)
t1 = d/v0 = -h / (v0 sin(α0)) = -15 / (700*(-0,075)) = -15 / -52,5 = 0,286s = 286 ms
Ok merci.
Que pensez vous de mon poste du
24-03-19 a 19:40 ?
Je n'obtiens pas le même résultat que toi pour z(t1)
Je ne comprends pas pourquoi tu cherches à calculer la position de B puisque apparemment on ne te la demande pas.
Je cherchais la position de B pour comparer mais apparemment ce n'est pas ce qu'il fait faire.
Et en effet je me suis trompé, je trouve z(t1) = 21m avec la constante g = 9,807 ms-2 (petit oubli de ma part mais qui ne change pas grand chose)
Mais après comment vous calculez  z0 ?
z0 ?
Comment faites-vous pour trouver ce résultat ?
J'utilise l'équation horaire :
z(t) = -(1/2)gt² + v0t + h
et je remplace la variable t par la constante t1=-h/(v0 sin(α0))
j'obtiens ainsi z(t1) en fonction de g, h, v0 et α0
et puisque la trajectoire en ligne droite s'arrête pour z=0 j'en déduis que δz0 = z(t1)
Mais en effet je trouve la même chose.
Je vous dis un grand merci pour toutes ces aides et ces explications que vous m'avez apporté.
MERCI !!
Lacryzz
J'ai en effet oublié le terme sin(α) dans l'équation horaire.
Mais cela n'impacte pas le résultat car il ne s'agit que d'un oubli passager de recopie : J'ai bien tenu compte de ce terme dans mon calcul.
Bonjour,
Dans les échanges, je pense qu'il y a lieu de corriger les écritures de la projection sur l'axe Oz du vecteur vitesse initiale par l'élève puis d'écrire sa transcription dans la formule de la chute libre des corps...
Un élève qui lit ce post sera induit en erreur à deux titres :
:- en prenant la formulation telle quelle est par absence d'effort et
- en ne prenant pas connaissance qu'avant la formule il y a la réflexion à tenir pour qu'avec les données et les lois de la physique supposées connues et acceptées on la démontre à nouveau en tenant compte des conditions initiales (on ne tient pas compte de la résistance de l'air) de sa validité pour l'exercice !
Cordialement
Bonjour,
Dans les échanges, je pense qu'il y a lieu de corriger le msg du 24-03-19 à 16:12 les écritures de la projection sur l'axe Oz du vecteur vitesse initiale par l'élève puis d'écrire sa transcription dans la formule de la chute libre des corps...
Un élève qui lit ce post sera induit en erreur à deux titres :
- en prenant la formulation telle quelle est par absence d'effort et
- en ne prenant pas connaissance qu'avant la formule il y a la réflexion à tenir pour qu'avec les données et les lois de la physique supposées connues et acceptées on la démontre à nouveau en tenant compte des conditions initiales (on ne tient pas compte de la résistance de l'air) de sa validité pour l'exercice !
Cordialement


