Niveau terminale

Le rayon de Bohr

Posté par
TitiR 03-04-18 à 13:04

Bonjour, j'aimerais de votre aimable

Que vaut le rayon de Bohr dans l'atome d'hydrogène à l'état fondamental ?

Je sais que les images sont interdites mais vu la taille du sujet je ne pouvais pas vraiment me permettre de tout recopier et je ne voulais pas omettre des données.

Je sais qu'à l'aide de la relation je peux trouver d²= (K * |q1-q2|)/FE

En revanche je ne sais pas à quoi peuvent servir les formules du document 4 pour trouver FE

Merci d'avance, bonne journée

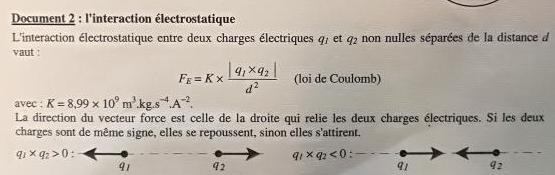
Le rayon de Bohr

***Image recadrée***

Posté par re : Le rayon de Bohr 03-04-18 à 13:05

aide*

Posté par re : Le rayon de Bohr 03-04-18 à 16:56

Hello

Sans considération sur le mauvais goût de tes remarques postées sur d'autres messages

"Je sais qu'à l'aide de la relation je peux trouver d²= (K * |q1-q2|)/FE "

J'ai du mal à cerner ce que tu sais mais tu retranscris avec une erreur l'expression fournie par le document 1:

$F_E = K \times \frac{|q_1\times q_2|}{d^2}$

"En revanche je ne sais pas à quoi peuvent servir les formules du document 4 pour trouver FE"

Le en revanche est inapproprié puisque ce qu'il y a par ailleurs, tu ne sembles pas le savoir non plus

Plus sérieusement, l'énoncé te demande de justifier que l'on ne se trouve pas dans le cas relativiste, c'est à dire que la vitesse de l'électron est suffisamment faible pour ce contenter de l'expression de la été de mouvement $\vec{p}= m\vec{v}$

Pour t'aider:

1) tu exprimes la 2nde loi de Newton qui te permettras de lier l'expression de F_E à la vitesse de l'électron

2) tu exploites le document 3 pour relier le rayon de la trajectoire à la vitesse de l'électron dont la caractéristique ondulatoire est donnée par la longueur d'onde de De Broglie

3) tu isoles v dans ces 2 équations et identifies les seconds termes ... tu auras trouvé l'expression du rayon de Bohr

Posté par re : Le rayon de Bohr 03-04-18 à 19:52

Bonsoir,

Tu as peut-être la "flemme" d'aider d'autres membres mais tu auras à recopier ton énoncé d'exercice (tu pourras juste insérer le schéma du modèle de Bohr).

Seuls les sujets de concours de plusieurs pages sont exemptés d'une recopie.

Merci

Posté par re : Le rayon de Bohr 04-04-18 à 09:31

Seconde loi de Newton

$\Sigma \vec{Forces} = m\vec{a}   (1)$

Dans le modèle de Bohr la trajectoire de l'électron est circulaire uniforme, donc

$\vec{a}= -\frac{v^2}{r}.\frac{\vec{Q_1Q_2}}{||\vec{Q_1Q_2} ||}$

où Q₁ est le point représentant le centre du noyau, supposé immobile
et  Q₂ est le point représentant l'électron

Soit Q₁Q₂ = r, rayon que l'on cherche à déterminer

Donc ici ,  avec  q1 = -q2 = +e , (1) devient:

$-K\frac{e^2}{r^2} = -m_e\frac{v^2}{r}$

Soit   $v^2 = \frac{Ke^2}{m_er}   (2)$

Par ailleurs, il est indiqué dans l'énoncé que la longueur d'onde associée à l'électron dans son état fondamental (correspondant au rayon de Bohr donc) était égale à la circonférence de son orbite.

Donc $2\pi r = \frac{h}{p}$ où h est la constante de Planck et p la quantité de mouvement de l'électron

On suppose l'électron non relativiste (on le vérifiera ensuite). Dans ce cas:   $\vec{p} = m_e\vec{v}$

Donc $2\pi r = \frac{h}{m_ev}$

Soit $v^2 = \frac{h^2}{4\pi^2m_e^2r^2}  (3)$

Et en identifiant (2) et (3) on obtient:

$\frac{h^2}{4\pi^2m_e^2r^2} = \frac{Ke^2}{m_er}$

Soit $r = \frac{h^2}{4\pi^2Ke^2m_e}$

Partant de là tu peux réinjecter dans (2) ou (3) pour trouver v

Le calcul numérique te fournit une valeur en 10⁶ m/s ce qui justifie le choix précédemment fait de se placer dans le cadre non relativiste (v << c  donc 1)

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Le rayon de Bohr

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique