Inscription / Connexion Nouveau Sujet
Le minimum de Déviation et la longueur d'onde
Bonjour à tous
J'ai un exercice merci beaucoup d'avance
Pour déterminer
 'la longueur d'onde lumineuse dans le verre on envoie un faisceau lumineux monochromatique émis par le
'la longueur d'onde lumineuse dans le verre on envoie un faisceau lumineux monochromatique émis par le
laser à la surface d'un prisme en verre d'indice de réfraction n.
1. Le rayon lumineux arrive sur la face (1) du prisme avec un angle d'incidence i ; puis il émerge de l'autre face avec un angle d'émergence i' , telle que i '= i . ( la condition pour avoir le minimum de déviation )
1-1) Rappeler les relations du prisme
==> •
•sin i=n sin r
• sin i' =n sin r'
• A=r+r '
• D=(i+i ')- A
C'est la loi de réfraction de Descartes
1-2)Montrer que l'expression de la longueur d'onde
 ' est :
' est :
; en déduire sa valeur
==> Une petite indication s'il vous plaît merci beaucoup d'avance
2)Qu'observe-t-on si on remplace la lumière monochromatique par la lumière blanche ?quel
est le nom de ce phénomène ?
=>La lumière blanche est une lumière polychromatique, c'est-à-dire composée de plusieurs couleurs. La décomposition des couleurs par un prisme est la dispersion.
la figure
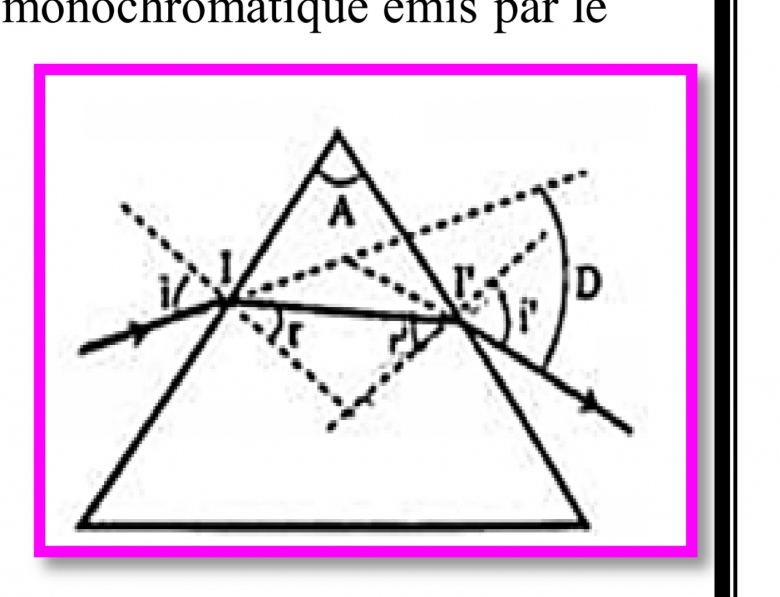
Merci beaucoup d'avance
Bonsoir
utilise les quatre relation du prisme dans le cas particulier :
i=i' et r=r'
Tu peux exprimer facilement r en fonction de A et exprimer i en fonction de (D+A).
Loi de Descartes...
Bonjour
Merci beaucoup de m'avoir répondu !
-Exprimer r en fonction de A:
A=2r ==> r=
-Exprimer i en fonction de ( A+D):
D=2i-A<=> A+D=2i
<=> i=
Merci beaucoup
Une petite indications s'il vous plaît merci beaucoup d'avance pour continuer
Merci beaucoup
Bonjour
Après une longue réflexion je trouve
•on a d'après la loi de Descartes :
Sin i =n sin r
Donc sin
Et n= donc :
sin
<=>
D'où
Merci beaucoup
Pour les autres questions c'est à dire question 1-1) et 2) et merci beaucoup
Je pensais cet exercice terminé puisque tu as résolu correctement l'exercice littéralement. S'il y a une application numérique à faire, il faut fournir les valeurs de A, D et  o.
o.
Bonjour
Merci beaucoup de m'avoir répondu !
Donc ma réponse à la question 1-1 et 2 sont justes?
L'énoncé malheureusement n'a pas donné aucune données pour les valeurs de A, D ,  '
'
Donc je vais données en Hazard A=30° et D=12° et  ' =30mm
' =30mm
Merci beaucoup
Tu précises que l'énoncé ne comporte pas de valeur numérique. Dans ces conditions, l'étude littérale que tu as faite est suffisante.
Tes autres réponses sont correctes. Peut-être ajouter à propos de la dispersion de la lumière blanche par le prisme : pour une même valeur de i, la déviation D dépend de la longueur d'onde.



