bonjour,

rappel: si F dérive du potentiel Ep alors: W_{F A->B} = - Ep = Ep(A) - Ep(B)

je suppose que B est le point du cercle d'altitude z_B = 0.

1) c'est assez confus:

Citation :
Par définition: WBS(P)= m*g*BS*cos

Citation :
m*g*BS*cos=m*g*zs

Citation :
z = 2R*cos

En attendant que tu postes l'énoncé, on peut faire des suppositions sur les questions posées...

Question 1
C'est clairement faux

Pour = 0° on doit trouver z_M = 0 m
Pour = 90° on doit trouver z_M = R
Pour = 180° on doit trouver z_M = 2R

Question 2
La vitesse en M ?
Oui, c'est cela, mais pour en faire une fonction de il faudrait avoir une bonne réponse à proposer pour la question 1 (afin de remplacer z_M par son expression)

Question 3
Le calcul est faux.
Mais l'expression finale est exacte...

Question 4
Il faut connaître v_S pour calculer v_B
Si v_B est exact, alors H est exact.

Veuillez m'excuser d'avoir scanner le sujet complet.
Je n'ai pas fait attention à ce point là dans  la FAQ et je pensais qu'il aurait été plus simple de scanner le sujet.
Dans tous les cas voici le sujet retapé et ainsi que les questions liées:

Un wagon d'un manège de parc d'attraction est propulsé par catapulte à une hauteur H. Il est ensuite abandonné sans vitesse initiale, dans une grande descente, puis effectue un looping de forme circulaire de 38 m de diamètre.
Dans la partie circulaire, la position de l'angle est représentée par l'angle .

On supposera que les frottements sont négligeable lors du mouvement du wagon qui sera assimilé à un point matériel

1. Exprimer l'altitude z du wagon en fonction du rayon R de la partie circulaire et de

2. Exprimer la vitesse de v_M du wagon en un point M repéré par cette angle

3. Que devient cette expression au sommet S de la boucle  ?

4. La valeur de la vitesse v_S en S doit être au minimum de 13,8 m.s^-1 pour que le wagon reste en contact avec le rail.
Quelle doit être la hauteur H pour que le wagon passe en S avec cette vitesse ?

Donnée : g=9,81 m.s^-1

Maintenant pour répondre à vos interrogations :

z correspond à l'altitude que peut avoir le wagon sur le cercle.
Si j'ai bien compris l'enoncé, cela veut dire que z est compris entre z_B et z_S et que sa valeur dépend de l'angle .
J'ai donc supposé que comme z est compris entre ces deux points, alors son énergie potentielle de pesanteur est aussi comprise entre E_pp(B) et E_pp(S)
Ainsi E_pp(B) = 0J et E_pp(S) = m*g*z_S

J'espère avoir été plus précis dans mes explications.

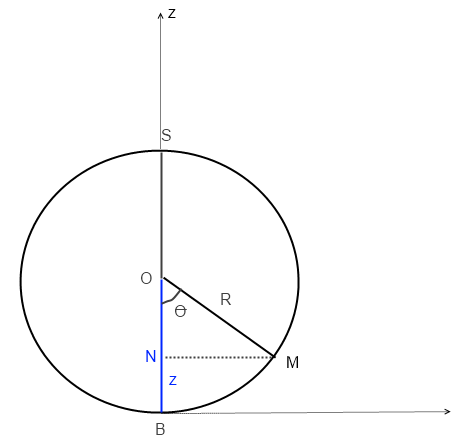
1) la question est purement géométrique

z = BN = BO - NO

et tu connais BO et NO en fonction de R et de l'angle

Merci beaucoup pour ton aide.

Si je ne me trompe pas, comme:

BO = R
ON = R*cos

on trouve que:

z = R - R*cos

soit:

z = R(1 - cos)

Du fait de cette expression, on en déduit que:

z_S = R(1 - cos)

Or, quand le wagon atteint le sommet du cercle, l'angle est égale à 180°

ce qui nous donne donc:

z_S = 2R

De part cette expression, on trouve bien:



Ainsi:



Je suppose que c'est la bonne démonstration ?

1) le point M a pour cote: z_M = R(1 - cos )

2) entre le point de départ et le point M, l' énergie mécanique se conserve (car on néglige les frottements)
donc pour trouver V_M il suffit décrire

mgH + 0 = mgz_M + 0.5V_M²

et de remplacer z_M par sa valeur en fct de

pourquoi t'embêtes-tu avec le point B ?
l'énerge mécanique se conserve entre deux points quelconques du mouvement, entre A et B, entre B et S, entre B et M etc..

3) immédiat (faire = dans la formule du 2, on suppose que H > R)

4) si Vs est donné alors tu trouves H

perdon:

on suppose que H > 2R

Bonjour,
j'ai le même exercice à faire mais je ne comprend pas très bien à partir de la question 2 ..
J'ai introduit le point A comme point de départ du wagon. Donc, l'énergie mécanique se conserve entre A et M
Em(A)=Em(M)
mgH=mg*zM+1/2v²M
Comme l'a dis précedemmentkrinn, j'ai donc remplacé zM par sa valeur:
mgH=mg*R(1-cos)+1/2v²M
Le problème est que je n'arrive pas à isoler vm.
Pouvez vous m'aider?
Merci d'avance

bonsoir,

tiens, un vieil exo

mgH = mg*R(1-cos O)+1/2 m v²_M (attention j'avais oublié un m)

tu passes mg*R(1-cos O) à gauche puis tu multiplies par 2/m et ça te donne v²

Je trouve que vM= racine(2gH-2gR(1-cos)
Est ce que c'est bon ?

oui, v = ( 2g(H - R(1 - cos O)) ) en mettant 2g en facteur

D'accord merci !
Par contre, pour la 4, je n'arrive pas à isoler H de l'expression v=(2g(H-R(1-cosO))) .
J'ai compris ce qu'il fallait faire mais c'est juste un problème de méthode. J'ai souvent du mal à isoler un terme d'une telle expression .
Peux tu m'aider ?

il vaut mieux partir de: mgH = mg*R(1-cos O)+1/2 m v²_M

en S: mgH = 2mg*R + 1/2 m v²_S

donc H = 2R + v²_S /2g
(on remarque que H > 2R ce qui est impératif car sinon la voiture n'atteint pas S)

si v_S >= 13,8 m.s-1 alors H >= ...

Bonjour !

J'ai le même exercice à faire. J'ai compris les deux premières questions mais j'ai en revanche du mal pour la question 3. Je ne vois ce que je dois faire pour trouver l'expression de Vs. J'ai essayé de comprendre les réponses données auparavant mais j'ai du mal à comprendre. SI quelqu'un pourrait m'aider...

Merci d'avance

bonsoir,

2) gH = g*R(1-cos )+1/2 v²_M pour tout point M situé sur la boucle

3) tu appliques la formule en S ( vaut alors ...) et tu trouve Vs² en fct de g R et H

Et dans la formule je remplace cos O par cos 180° ?!

exact

sachant que cos 180° = ...

Cos 180° = -1

oui