Inscription / Connexion Nouveau Sujet
Le bon angle (je bloque dans deux questions)
Bonsoir,
Pouvez-vous m'aider pour la question 2a et b
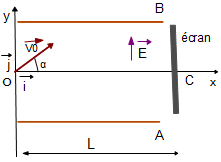
Un électron pénètre dans un condensateur plan comme indiqué sur la figure ci-dessous .
1.a. établir l'équation de la trajectoire de cet électron .
a. quelle est la nature de cette trajectoire ?
2.a.exprimer littéralement la condition que doit vérifier α pour que l'électron arrive au centre C de l'écran .
b.calculer α pour L=15cm
Données :
E=790V.m^-1 ;
masse électron : m=9,1*10^(-31)kg
v0=1,0*10^7m.s^(-1)
Ce que j'ai fais:
J'ai tout réussi sauf la question 2a et b
La trajectoire j'ai trouvé y = (-1/2)(-e/m.E).t^2+vo.sin(a).t
Merci d'avance
et bonne soirée
Bonjour,
Pour pouvoir être aidé(e), le minimum consiste à poster un énoncé complet...
Ce serait très utile, et même sans doute nécessaire, d'avoir la figure :
Pour apprendre à insérer une image, une figure, un schéma, un graphique, un tableau (pas un énoncé !) clique sur la maison 
![]()
Qu'as-tu répondu aux premières questions ?
Ce que tu proposes n'est pas l'équation de la trajectoire y(x) mais est l'équation horaire y(t) selon l'axe vertical, probablement.
Ce serait bien que tu expliques les signes choisis ; je me pose des questions.
Pour bien écrire sur le forum les expressions mathématiques, il ne faut pas oublier les parenthèses nécessaires. Il en manque certainement.
Quelle est la nature de la trajectoire entre les plaques du condensateur ?
Où se trouve l'écran par rapport à la sortie du condensateur ?
Qu'est-ce que L ?

Merci de me répondre 
J'ai posté à 22h46 et j'avoue que mon cerveau est mort à partir de 21h du coup je fais des erreurs bêtes 
La prochaine fois je dors tôt et je me lève tôt c'est mieux !
!
Voici l'image:
Je redis : ce que tu as posté n'est pas l'équation de la trajectoire.
C'est un élément de l'équation horaire de la particule.
Quelles sont tes réponses aux questions 1a et 1b ?

la 1.a
m.a(vecteur)=F (vecteur)
m.a (vecteur)= q.E(vecteur)
m.a (vecteur)=-e.E(vecteur)
a(vecteur)=(-e/m)Ey (vecteur)
Par projection
ax=dvx/dt=0
ay=dvy/dt=-e*(E/m)
Par intégration
vx =constante donc vx=Vo.cos 
vy=-e*(E/m)t+Vo.cos 
x(t)=Vo.cos  t
t
y(t)=(-1/2)*(-e*(E/m))t2+Vo.sins  t
t
b) la nature de cette trajectoire est une parabole
vy=-e*(E/m)t+Vo.cos

Il y a une erreur (probablement de recopie)
________
y(t)=(-1/2)*(-e*(E/m))t2+Vo.sins
 t
tPourquoi y a-t-il deux fois le signe "moins" ?
________
Mais ceci ne donne toujours pas l'équation de la trajectoire y(x) ; je pense que l'on attend de toi autre chose qu'une équation paramétrique.

F=qE
mx"=qE et my"=qE
x"=0 et y"=q/m E
x'= C1 et y'=qtE/m + C2
on trouve C1 = V0cos( )
)
et C2=V0sin( )
)
x'=V0cos( ) et y'=qtE/m + V0sin(
) et y'=qtE/m + V0sin( )
)
x=V0cos( )t et y'=qt²E/2m + V0sin(
)t et y'=qt²E/2m + V0sin( )t
)t
Au signe pret... on trouve alors avec x(t)
t=x/V0cos( )
)
tu injectes la valeur de t dans y(t) pour trouver y(x)
Après tu calcules dy(x)/d , et tu montre que y= maxi si
, et tu montre que y= maxi si  =45°
=45°
Au signe pres parce que jai laissé q, et que j'ai fait le calcul a la va vite. Donc je ne duis pas certain...j'ai pas posé le calcul sur feuille quoi.
Je vois angle idéale. Pour moi c'est quand y(alpha)=maxi...
Cordialement..
Eh bien, cela aurait été mieux de ne pas le faire "à la va vite" et de commencer par lire l'énoncé : ce n'est pas cela que l'on cherche

Ben je lui ai donner la trajectoire de l'e-. Il a juste a remplacer q par -e.
Il faut y=0 et x=L
Tu résouds y(x)=y(L)=0 et tu trouve la valeur de l'angle.
Voili voulou  )
)
Ps a M. Coll, il serait également appréciable que quelq'un puisse aussi m'éclairé. Sur tout les sujets que j'ai deja posté, jamais on ne m'a repondu correctement. Toujours ete remballé. Et pourtant je me fait chier a bien presenter mon probleme.
Cordialement, The Bartov 
Donc Hermione, le probleme me semble résolu.. y a til encore des probleme ? 
Excusez moi si vous avez mal pris mes propos. Mais cela ne change rien au problème. C'est avec plaisir que je donne mon aide aux autre. La seule chise que je demange, c'est un peut de considération. Parce que j'ai déjà été banni pour multi post, alors qu'il n'y avait aucune raison. Je voulais qu'un physiscien m'explique une idee mathematique : le calcul du flux. On a fermé un premier topic pour "Hors Sujet"... je refait le topic en exposant clairement que je souhaitais un point de vue physiscien. => banni pour 10jours.
Et là, en utilisant un peu de vocabulaire non fleurit, j'obtient un avertissement... je ne comprends pas. Pourtant je ne vous ai ni insulté, ni attaqué (je vous vouvoie. C est pour dire). A moins que vous n'aimez pas le verbe "chier"
... remplacez le donc par "casser les pieds", et relisez le message, et reconsidérez mon message.
Donc monsieur Coll, pouvez vous jeté un coup d'oeil à mon topic, dans le niveau supérieur en chimie. C est un dosage de l'axide acetique par la soude. Mon probleme est bien posé, et il est clair et net.
amicalement, theBartov
Bonjour,
Je remonte un vieux post car je suis bloquée à cet exercice à la question 2a.
Je donne mes réponses aux question précédentes :
1: a : équation de la trajectoire : y = (eE/2m)*(x/v(0)cos(a))² + v(0)sin(a)
1: b: la trajectoire est une parabole
2: a: j'essaye vainement d'isoler a, mais je bloque arrivée à sin(a)*cos²(a) =(-eEx²)/(2m*v(0)^3)
Avec e : charge élémentaire de l'électron
E : valeur du champ magnétique
m : masse de l'électron
a : angle alpha visible sur la figure des messages précédents.
Merci d'avance de vos réponses
Bonsoir,
1.a)
Quelle est la direction et le sens de la force exercée par le champ électrique sur l'électron ?
Conséquence sur les coordonnées de l'accélération ?
Peux-tu indiquer ce que tu trouves pour
x(t) = ?
y(t) = ?
L'équation de la trajectoire y(x) que tu indiques est fausse.
1.b) Oui, un arc de parabole.
2.a) Avec une équation correcte de la trajectoire ce sera plus facile...

1: a: Sens et direction de la force exercée par le champs électrique sur l'électron : vertical vers le haut, comme le vecteur E sur le schéma précédent ?
Je trouve pour x (t) : v (0) t cos alpha
Et pour y (t) : (e*t^2*E)/(2m) + v (0) sin alpha
Merci !
1.a : 
Un électron est porteur d'une charge négative
Le sens de la force est faux
Donc le sens de l'accélération est faux
Donc y(t) est faux pour cette première raison
1.b
x(t) : d'accord
y(t) : non pour une deuxième raison : tu as mal intégré la vitesse

Du coup on a y=(-e*E*t^2)/(2m) + v0 sin alpha ?
et donc comme comme équation de trajectoire y=(-e*E*x^2)/(2m*v0^2*cos^2 alpha) + v0 sin alpha ?
Si c'est ca ca ne change pas grand chose dans mon équation ...
Je me suis trompée.
Y = (e*t^2*E)/(2m) + v0*t*sin alpha
Donc equation de la trajectoire :
Y = (e*E*x^2)/(2m*v0^2*cos^2 alpha) + vo*sin alpha*(x/v0*cos alpha)
C'est bien ca ?
Tu y arrives...
1.a)
x(t) = v0.cos( ).t
).t
y(t) = (- 1/2).(e.E/m).t2 + v0.sin( ).t
).t
D'où l'équation de la trajectoire :
y(x) = (- 1/2).(e.E/m).x2/[v0.cos( )]2 + tan(
)]2 + tan( ).x
).x
Notes :
. v0.sin( )/[v0.cos(
)/[v0.cos( )] = tan(
)] = tan( )
)
. mais, pour la question 2, tu pourras écrire tan( ) sous la forme sin(
) sous la forme sin( )/cos(
)/cos( )
)
1.b)
Un arc de parabole.
À toi pour la suite, je t'ai donné une indication pour la résolution...

Je suis votre discussion depuis le début, et j'ai beau tourner l'équation de la trajectoire dans tous les sens, impossible d'isoler alpha...
HELP ! J'aimerais un indice  Faut-il factoriser, résoudre un système ? Car à la fin je trouve :
Faut-il factoriser, résoudre un système ? Car à la fin je trouve :
(- 1/2).(e.E/m).L^2/[v0.cos(a)]^2 + tan(a).L = 0
(- 1/2).(e.E/m).L^2/[v0.cos(a)]^2 + sin(a)/cos(a).L = 0
(L/cos(a))(-e.E.L/[2.m.v0^2.cos(a)]+sin(a)) = 0
(-e.E.L/[2.m.v0^2.cos(a)]+sin(a)) = 0
(-e.E.L/[2.m.v0^2.cos(a)]= sin(a)
2.m.v0^2.cos(a).-sin(a) = -e.E.L
cos(a).sin(a)= e.E.L/2.m.v0^2
Je ne vois comment isoler alpha par la suite...
Je l'avais oublié celle-là ! Merci énormément, je vais enfin pouvoir dormir tranquillement (le problème trottait dans ma tête depuis quelques jours !)
Bonne fêtes 
bonjour, j'utilise ce post car j'ai le meme exercice et je suis bloquer lorsque j'ai mon équation
y(t)= (-1/2)(e.E/m).t^2+vo.sin( ).t
).t
je ne comprend pas comment obtenir x au lieu du t
[url]F=qE
mx"=qE et my"=qE
x"=0 et y"=q/m E
x'= C1 et y'=qtE/m + C2
on trouve C1 = V0cos()
et C2=V0sin()
x'=V0cos() et y'=qtE/m + V0sin()
x=V0cos()t et y'=qt²E/2m + V0sin()t
Au signe pret... on trouve alors avec x(t)
t=x/V0cos() [/url]
ceci je ne le comprend pas mais je vois toutefois que l'explication de ma question est ici ( enfin je pense)
ah non c'est bon j'ai trouver !
par contre je suis bloquer pour isoler 
(- 1/2).(e.E/m).L^2/[v0.cos(a)]^2 + tan(a).L = 0
(- 1/2).(e.E/m).L^2/[v0.cos(a)]^2 + sin(a)/cos(a).L = 0
(L/cos(a))(-e.E.L/[2.m.v0^2.cos(a)]+sin(a)) = 0
(-e.E.L/[2.m.v0^2.cos(a)]+sin(a)) = 0
(-e.E.L/[2.m.v0^2.cos(a)]= sin(a)
2.m.v0^2.cos(a).-sin(a) = -e.E.L
cos(a).sin(a)= e.E.L/2.m.v0^2
comment passe-t-on de la 2eme a la 3 eme ligne ?
vous etes sur qu'il n'y a pas d'erreur ?
merci d'avance, cela fait vraiment beaucoup de temps que j'y suis dessus !!
ah ok et à la fin quand j'obtient
sin(2a) = e.E.l/ (mv0²)
pour trouver a pour l = 15 , je remplace par les valeur, j'obtient un résultat et ce resultat je lui fais "arcsin" sur la calculatrice. Ce que j'obtient je le divise par 2 pour trouver a
mais le soucis c'est que e = nombre d'electron c'est ça ? mais il n'est pas donnés
e est traditionnellement la valeur de la charge électrique unité (positive), celle du proton.
-e est donc la charge électrique de l'électron

et aussi Fe (vecteur) = e.E ou -e.E
cela dépend si Fe(vecteur) a un sens opposé a E(vecteur) ou si Fe(vecteur) est dans le meme sens de E (vecteur)
ici c'est Fe (vecteur) = -e . E mais je n'ai pas compris pourquoi ?
merci
juste Fe (vecteur) = -e . E donc Fe(vecteur) a un sens opposé a E(vecteur) mais comment on le sais ici ? svp
Mais on le sait parce qu'on multiplie le vecteur par un nombre négatif -e
Un proton subit une force dans le même sens que le champ électrique
Un électron subit une force dans le sens opposé au champ électrique

donc en fait a chaque fois que c'est un electron c'est la formule Fe= -e. E
on ne peut pas douter avec Fe = e.E
Y'a également un point que je souhaiterais éclaicir :
losque au tout debut on détermines les composantes de a (vecteur) comment on sait que c'est ay qui est égal à (-e.E)/m et pas
ax
?
La "formule" est
: force à laquelle est soumise une particule de charge électrique q dans un champ électrique
Pour un proton : q = e
Pour un électron : q = -e

ah d'accord parfait merci !!
et
Y'a également un point que je souhaiterais éclaicir :
losque au tout debut on détermines les composantes de a (vecteur) comment on sait que c'est ay qui est égal à (-e.E)/m et pas
ax
?
Quelle est la direction et le sens de la force ?
Puis, deuxième loi de Newton : quelle est la direction et le sens de l'accélération ?

direction verticale
sens vers le haut
en conséquence d'apres la 2 eme loi de Newton, le sens et la direction de l'accélération sont identique à ceux de la force

Pour la force :
Direction : parallèle à l'axe Oy
Sens : opposé à celui de l'axe Oy puisque a le sens de l'axe Oy et que la particule est un électron de charge électrique négative
L'accélération a même direction et sens que la force.

ah okkkk !
et en fait le sens et direction de la force va nous donner les composantes c'est ca ?
imaginons que la force aurait été parallèle à l'axe des abscisse, on aurait mis ax = .. au lieu de ay ?

 sin(a)
sin(a) 
 -1,602.10-19 C
-1,602.10-19 C

