Inscription / Connexion Nouveau Sujet
La portée d'une flèche
Bonjour,
Un solide supposée ponctuel est lancé d'un point O dans le plan O,
,
avec une vitesse v0 = 20 m/s dans le champ de pesanteur terrestre sup. constant de valeur g0 = 10 m/s
On cherche à atteindre à partir du poin O le point M' (10, 10, 0)
- Déterminer les angles de tir possibles
Au départ j'ai fait les formules de la "flèche qui atteint le sommet" soit portée : xS = 10 et yS = 10 en isolant 
et on trouve 1 = 15° et 2= 45°
mais je ne pense pas que c'est le bon raisonnement...
Une petite aide me permettrait sûrement de me débloquer pour le reste de l'exercice.
Merci et bonne fin de week-end.
a = - g ;
x(t)=v0 cos (alpha) t ;
y(t)=-g/2t^2+ v0 sin (alpha) t; y(x)= -g/2 * x^2 /(v0 * cos(alpha))^2 + x tan (alpha);
Il s'agît ici de faire en sorte que y(10)=10 (M' appartient ici à la trajectoire...);
re-bonjour,
voici la petite aide :
il faut écrire en fonction de l'angle de tir les équations horaires x(t) et y(t) de la flèche (pas dur, elles figurent dans tous les manuels de terminale...), puis éliminer le temps t (facile aussi, on exploite x(t) = V0.cos.t soit t = x/(V0cos), que l'on reporte dans y(t) pour en déduire y(x), équation de la trajectoire).
Ensuite il faut écrire que cette trajectoire doit passer par le point P de coordonnées (10, 10). Tu va ainsi obtenir une équation qui va donner l'angle , et en effet il y a deux solutions : une valeur plus petite que 45° (on appelle ça "tir tendu") et la valeur complémentaire, plus grande que 45° ("tir en cloche").
Dans le premier cas le sommet S de la trajectoire n'est pas encore atteint, dans le second il est dépassé puisque la flèche retombe avant d'atteindre P.
A toi de faire les calculs...
..... Au passage, pour résoudre ensuite l'équation obtenue, tu pourrais prendre en compte le fait que 1/(cos(x))^2=1+(tan(x))^2 et ensuite poser A=tan(alpha) (Et alors, Trinôme du Second Degré .....).....
Ah, je ne trouve pas ça...
Algébriquement, l'équation à résoudre est bien celle donnée par REMY_K : y = -g.x2.(1+tan2)/2/V02 + x.tan.
Avec x = y = 10, et en posant tan = X, j'obtiens numériquement 5.X2/4 - 10X + 45/4 = 0. Je te passe les détails du calcul, les racines sont X1 = 1,354 soit 1 = 53,6°, et X2 = 6,646 soit 2 = 81,4°.
Cela dit, moi aussi j'ai fait une erreur dans mon post de 12h54, en te donnant une mauvaise indication : les angles 1 et 2 ne sont complémentaires que si le point de départ et le point d'arrivée sont à la même hauteur, càd, dans le cas de cet exercice, si le point d'impact P avait eu une ordonnée nulle comme celle du point départ O. Si le point P est plus haut, un raisonnement évident (mais que je n'ai pas fait) indique qu'il faut relever l'arc, donc que la symétrie des deux directions de tir par rapport à 45° n'est plus vraie. Désolé...
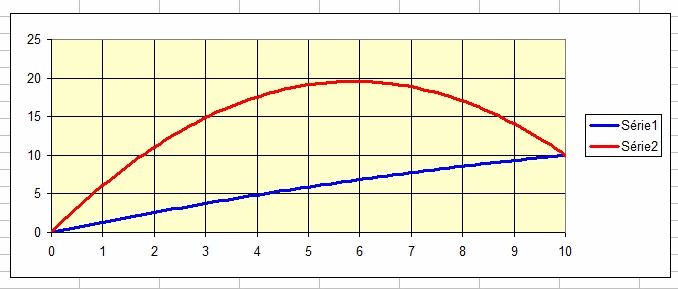
Pour me faire pardonner, voici ci-dessous les trajectoires tracées avec excel, pour les deux angles trouvés ci-dessus. la courbe bleue correspond au tir tendu ( = 53,6°) et la rouge au tir en cloche ( = 81,4°).
Heureusement pour toi, il est encore temps de corriger.
A bientôt peut-être sur ce forum.
B.B.
Annuler
connectez vous