Inscription / Connexion Nouveau Sujet
la modélisation des frottements lors d'une chute libre
Bonjour à tous et toutes,
Voici le sujet de mon devoir à rendre prochainement, j'ai quelques pistes mais je pêche parfois sur la tournure de certaines questions. Je vous remercie par avance pour votre aide.
Un projectile que l'on assimilera à un point matériel de masse m=1kg est lancé avec une vitesse vo=15m/s. On fixera l'origine du repère Oxyz associé au référentiel terrestre qui sera supposé galiléen au niveau de la position du point M au moment de son lancement.
Le vecteur vitesse à l'instant initial noté vo appartient au plan xOz. L'axe Oz est l'axe vertical ascendant et Ox un axe horizontal. On note α l'angle (ex, vo) qui sera pris entre 0 et 90°. On supposera que le champ de pesanteur terrestre est uniforme et d'intensité égale à 2 9,81 m/s2
A) Les frottements de l'air sur le projectile sont négligés :
1) Déterminer l'équation de la trajectoire du projectile.
Ok compris fait
2) Déterminer le lieu des points du plan vertical contenant le mouvement, susceptibles d'être atteints par le projectile pour une vitesse initiale vo donnée.
Est-ce que c'est le sommet de la parabole qui est demandé à cette question, j'avoue que j'ai eu du mal à comprendre la tournure de la question.
3) Montrer alors qu'un point atteint peut l'être avec deux valeurs α1et α2 différents. Un schéma illustratif est demandé.
Pour 2 angles identiques vis-à-vis de 45°, la portée est identique. La portée : z=0 est atteinte
B) Une première modélisation des frottements de l'air :
Les frottements de l'air sont pris en compte dans cette partie. On considère que dans le domaine de vitesse étudié, la force qu'exerce l'air sur le projectile est proportionnelle à la vitesse avec un coefficient de frottement h =1USI dans les unités du système international.
On prendra 45°.
1) Montrer que le projectile (s'il n'est pas contraint : c'est-à-dire que l'on considérera qu'il est jeté du haut d'une falaise de hauteur supposée « infinie ») tend vers une vitesse limite que vous noterez V1 et que vous exprimerez en fonction des données.
Ici on cherche les équations de v en x et y et ensuite on cherche ensuite la limite
2) Qualifier le mouvement au bout d'un temps très long.
Lorsque la vitesse limite est atteinte peut-on dire que le mouvement est rectiligne uniforme ?
3) On pose Ʈ=h/m
Quelles sont les dimensions de h et de m ? Que représente physiquement la constante Ʈ ?
Ok compris fait
4) Calculer Ʈ et la norme du vecteur que l'on notera V1.
On calcule Ʈ avec les vitesses précédentes
Pour la norme, j'utilise la racine carré des coordonnées au carré
Dorénavant, les expressions littérales demandées feront intervenir Ʈ, V1, vo et α comme constantes.
5) Etablir les expressions littérales des coordonnées du projectile en fonction du temps.
Intégration des vitesses aux différentes coordonnées
6) Donner l'allure de la trajectoire. Montre qu'elle admet une asymptote dont on
donnera l'équation littérale puis numérique. Représenter sur un même graphe, sans
calculs, l'allure qu'aurait la trajectoire s'il n'y avait pas de frottements.
?
7)
a. Donner l'expression littérale de l'instant ts , où le projectile atteint le
sommet de sa trajectoire, l'abscisse xs de ce sommet, ainsi que la vitesse
vs du projectile en ce point.
?
b. Donner les expressions ts et la norme vs la norme du vecteur vs et des
coordonnées du sommet dans le cas où les frottements sont négligés. On
donnera ces expressions en fonction de g , vo et Ʈ .
?
c. Etablir un tableau comparatif des valeurs numériques de ts , vs et des
coordonnées du sommet dans les deux situations étudiées.
8)
a. Déterminer numériquement l'instant tp où le projectile repasse à la même
altitude que celle de son point de départ, ainsi que l'abscisse xp
correspondante qui est en fait la portée du tir.
?
b. Donner les expressions de tp et xp dans le cas où les frottements sont
négligés en fonction de g , vo et α.
?
Bonjour
Pour 2 : il faut pour une valeur constante de Vo faire varier l'angle entre zéro et pi/2. Tu trouves facilement de l'aide sur le net en tapant : parabole de sûreté.
Pour 3 : écrit l'équation de la trajectoire. Pour un point donné de celle-ci de coordonnées (x1,y1) et une valeur donnée de Vo, correspond 2 valeurs possibles de l'angle.
Pour la chute verticale avec frottement : l'intensité de la force de frottement, initialement nulle augmente en fonction de la vitesse donc commence par augmenter au cours de la chute. Que se passe-t-il lorsqu'elle devient de même intensité que le poids?
Je te laisse réfléchir et proposer une solution.
Bonjour,
@ sheigh : en vertu des règles du forum, peux-tu mettre à jour ton profil :
![]() [***A LIRE AVANT D'AGIR***] Règles du forum
[***A LIRE AVANT D'AGIR***] Règles du forum
gbm
Bonjour,
@ sheigh : en vertu des règles du forum, peux-tu mettre à jour ton profil
J'ai rectifié, j'espère bien.
Pour continuer
A
2) Déterminer le lieu des points du plan vertical contenant le mouvement, susceptibles d'être atteints par le projectile pour une vitesse initiale vo donnée.
Avec ce que vous avez marqué, je me suis dit qu'il fallait peut-être s'aider de l'éq de la trajectoire et faire varier
3) Montrer alors qu'un point atteint peut l'être avec deux valeurs ?1et ?2 différents. Un schéma illustratif est demandé.
Avec vos explications, pour atteindre 1 pt de coordonnées (x1,y1) avec une vitesse vo, l'angle doit être solution de l'équation de la trajectoire.
J'ai posé u=tan
B
Pour répondre à votre question, lorsque la vitesse devient de même intensité que le poids, l'accélération devient nulle et la vitesse tend vers une constante = vitesse limite ?
1) Montrer que le projectile (s'il n'est pas contraint : c'est-à-dire que l'on considérera qu'il est jeté du haut d'une falaise de hauteur supposée « infinie ») tend vers une vitesse limite que vous noterez V1 et que vous exprimerez en fonction des données.
avec
-1)
et
v1=g*
2) Qualifier le mouvement au bout d'un temps très long.
On est en régime asymptotique
3) On pose ?=h/m
Quelles sont les dimensions de h et de m ? Que représente physiquement la constante ? ?
Ok compris fait
4) Calculer ? et la norme du vecteur que l'on notera V1.
On calcule ? avec les vitesses précédentes
Pour la norme, j'utilise la racine carré des coordonnées au carré
5) Etablir les expressions littérales des coordonnées du projectile en fonction du temps.
J'ai intégré la vitesse vz que j'ai trouvé précédemment mais pour les conditions initiales à t=0, z=infini d'après l'énoncé, ce qui me bloque.
6) Donner l'allure de la trajectoire. Montre qu'elle admet une asymptote dont on
donnera l'équation littérale puis numérique. Représenter sur un même graphe, sans
calculs, l'allure qu'aurait la trajectoire s'il n'y avait pas de frottements.
____________________
***Edit gbm : ton profil n'est tjs pas à jour***
Pour la parabole de sûreté et les deux valeurs possible de l'angle de tir pour atteindre un point donné : cela est bien expliqué ici ; commence par étudier ce document puis pose des questions complémentaires si tu le juges utile :
![]()
Questions B1 et B2 : je pense que l'énoncé demande une justification qualitative. Il ne s'agit pas pour l'instant de résoudre les équations différentielles dont les composantes du vecteur vitesse sont solutions. Il suffit de partir de l'équation différentielle résultant de l'application du principe fondamental de la dynamique projeté sur un axe vertical orienté vers le bas :
Au fur et à mesure de la chute, la vitesse augmente, h.v augmente, l'accélération diminue jusqu'à devenir nulle : ce cas limite correspond donc à une vitesse maximale possible (vitesse limite) telle que :
Lorsque cette limite est atteinte, le mouvement est vertical, rectiligne et uniforme.
A partir de B5, il faut projeter la relation fondamentale de la dynamique sur les deux axes. Il faut utiliser la méthode utilisée en partie A en ajoutant la force de frottement :
Cela fait deux équations différentielles à résoudre.
N'y aurait-il pas une erreur de recopie de l'énoncé ? La constante  n'est-elle pas plutôt définie par :
n'est-elle pas plutôt définie par :
???
Bonjour,
N'y aurait-il pas une erreur de recopie de l'énoncé ? La constante
 n'est-elle pas plutôt définie par :
n'est-elle pas plutôt définie par :Ola oui, j'ai bien mal recopié l'énoncé.
Si j'ai bien compris.
Partie A
1) ok
2) je dois rechercher la parabole de sûreté où les points sont accessibles pour un angle et une vitesse donnée.
3) grâce à l'équation trouvée précédemment au 1) je dis que la cible est atteinte en y=0 , ce qui me fait obtenir deux angles . Le schéma attendu est parabole = tir en cloche et une autre tir tendu.
Partie B
1 et 2) je remets votre explication
Il suffit de partir de l'équation différentielle résultant de l'application du principe fondamental de la dynamique projeté sur un axe vertical orienté vers le bas :
Au fur et à mesure de la chute, la vitesse augmente, h.v augmente, l'accélération diminue jusqu'à devenir nulle : ce cas limite correspond donc à une vitesse maximale possible (vitesse limite) telle que :
h.\overrightarrow{v_{1}}=m.\overrightarrow{g}
Lorsque cette limite est atteinte, le mouvement est vertical, rectiligne et uniforme.
3)Ok
4)
5) à partir de
m*dvx/dt=-h*vx
mdvy/dt=h*vy-m*g
on intègre jusqu'à x / y et on utilise les conditions initiales
6) on prend x(t) et on fait tendre t vers plus l'infini =
7) a)b sommet de la trajectoire = point de la trajectoire où la tangente est horizontale
dy/dt=0
même frottement et sans frottement
c) tableau comparatif avec valeurs numériques frottements / sans frottements
8) Par contre ici je n'ai pas compris
Merci.
***Niveau mis en accord avec le profil***
Je t'ai induit en erreur au niveau des notations : l'axe vertical est, selon l'énoncé, l'axe (Oz) alors que j'ai considéré qu'il s'agissait de l'axe (Oy) . Facile de corriger...
question 7a) : la date de passage au sommet et la vitesse au sommet sont différentes selon que l'on considère ou non l'existence de frottements. Il faut que tu revois cela.
Question 8 : tp est la valeur de t strictement positive telle que z=0 puisque, à l'instant initial : z=0 et x= 0. Evidemment, la portée xp est beaucoup plus faible en présence de frottement.
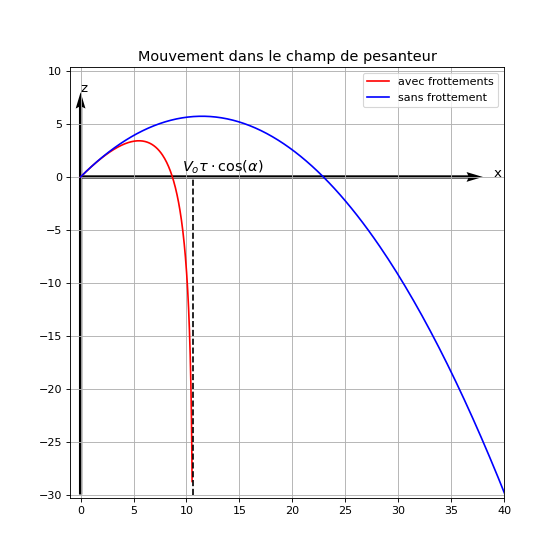
Pour illustrer tout cela, voici le tracé des deux trajectoires. Ton énoncé considère une valeur de h très élevé ; en pratique, l'écart de comportement entre les deux cas est plus faible. Il faut aussi savoir que ce modèle de force de frottement est assez peu réaliste dans l'air ; en réalité, la force de frottement est proportionnelle au carré de la vitesse mais les calculs sont beaucoup plus compliqués...
Bonjour,
7a) : la date de passage au sommet et la vitesse au sommet sont différentes selon que l'on considère ou non l'existence de frottements. Il faut que tu revois cela.
D'accord!
Question 8 : tp est la valeur de t strictement positive telle que z=0 puisque, à l'instant initial : z=0 et x= 0. Evidemment, la portée xp est beaucoup plus faible en présence de frottement.
Pour illustrer tout cela, voici le tracé des deux trajectoires. Ton énoncé considère une valeur de h très élevé ; en pratique, l'écart de comportement entre les deux cas est plus faible. Il faut aussi savoir que ce modèle de force de frottement est assez peu réaliste dans l'air ; en réalité, la force de frottement est proportionnelle au carré de la vitesse mais les calculs sont beaucoup plus compliqués...
merci pour l'ensemble des explications qui m'a apporté un peu plus de clarté à cette partie du devoir.
Bonjour,
J'ai un petit problème à la question 8a, j'ai du mal à extirper tp et lui donner une valeur:
Je pars de 0=*(v0*sin
+g*
)(1-exp(-tp/)-g*
*tp
Merci par avance.
À ce que je comprends de l'énoncé, les expressions littérales de la portée xp et du temps tp correspondant ne sont demandées qu'à la question 8b) lorsque les frottements sont négligés. Il s'agit d'un classique du cours de terminale. En tenant compte des frottements, l'énoncé, à la question 8a) demande seulement une détermination numérique. Heureusement car l'équation vérifiée par tp fait intervenir à la fois tp et : pas d'expression littérale simple de tp !
Il suffit donc d'écrire l'équation vérifiée par tp ; de remplacer vo, g, et
et  par leurs valeurs numériques puis d'utiliser une calculatrice scientifique ou un programme scientifique sur ordinateur pour obtenir la valeur numérique de tp. Facile alors d'obtenir la valeur numérique de xp.
par leurs valeurs numériques puis d'utiliser une calculatrice scientifique ou un programme scientifique sur ordinateur pour obtenir la valeur numérique de tp. Facile alors d'obtenir la valeur numérique de xp.
Heureusement car l'équation vérifiée par tp fait intervenir à la fois tp et \exp\left(-\frac{t_{p}}{\tau}\right) : pas d'expression littérale simple de tp !
Il suffit donc d'écrire l'équation vérifiée par tp ; de remplacer vo, g, et par leurs valeurs numériques puis d'utiliser une calculatrice scientifique ou un programme scientifique sur ordinateur pour obtenir la valeur numérique de tp. Facile alors d'obtenir la valeur numérique de xp.
Bonjour, merci.


 équivalences des systèmes de niveaux scolaires
équivalences des systèmes de niveaux scolaires
 en post-bac
en post-bac