Inscription / Connexion Nouveau Sujet
la mécanique de newton : dm
bonsoir,
pour jeudi j'ai un dm composé de 2 exercices, sur la mécanique de newton. j'ai déjà réussis à faire le premier, mais je bloque sur le 2ème. j'espère que vous pourrez m'aider. voici l'énoncé :
on sidère un repère (O;i;j). A la date t=0s, une particule chargée, de masse m, arrive au point 0. son vecteur vitesse est alors 
(o) = v(0)
; avec v(o)= 20.0 km/s.
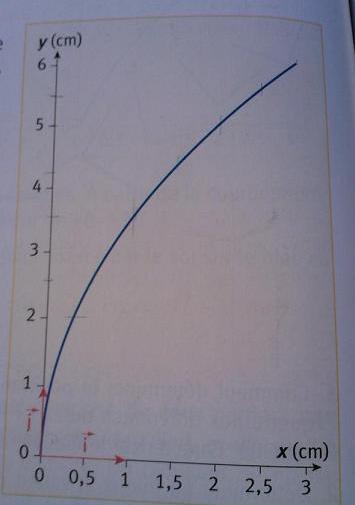
a partir de cette date, elle subit de la part d'autres charges une force électrique constance (vecteur F)=F
; le poids de la particule est négligeable devant cette force. On a représenté la trajectoire de la particule dans le repère (O:i:j)
1) tracer sur le schema le vecteur (o) (10 km/s-1 étant représenté par 005 cm ). préciser le signe de F
2) a partir de la 2eme loi de nexxton, caractériser le vecteur accélération de la particule. quelle est la propriété vérifiée par la composante vy de la vitesse de la particule ?
3)a. justifier qu'à partir de la valeur de vy(t) et de la tangente à la trajectoire à ma date t, on puisse construire sur le graphique le vecteur vitesse de la particule a la date t.
b. représenter sur le schèma le vecteur vitesse aux dates t3 et t5 pour lesquelles y=3.0 et5.0 cm. calculer t5-t3
C. a partir du schema, déterminer Vx en ces deux points . en déduire une valeur approchée de l'accélération de la particule pour y=4.0 cm
d. la particule est un ion He2+ de masse m=6.7 * 10-27kg. donner une valeur approchée de F.
La 1, je suppose que tu sais la faire...
Pour la 2, la force étant selon l'axe x (), il en est de même pour l'accélération :
ax = F / m
ay = 0
vx = (F/m)t + v0x = (F/m)t car v0x = 0
vy = v0y = v(0)
vy est constante
x = (F/2m)t2 + x0 = (F/2m)t2 car x0 = 0
y = v(0)t + y0 = v(0)t car y0 = 0
x = (F/2m)t2 
D'où :
Jusque là, ça va ?
Pour la 3, c'est un peu plus difficile à expliquer...
La vitesse est portée par la tangente à la trajectoire. Le problème, c'est comment déterminer son amplitude (sa longueur)...
La vitesse étant la somme de 2 vecteurs vx et vy, on peut la déterminer seulement avec vy puisque vy est constant, alors que vx ne l'est pas (dépend du temps).
Il suffit de tracer la tangente en un point et de tracer la vitesse vy = v(0) (donc parallèle à Oy, vers le haut). On trace une parallèle à Ox à partir de l'extrémité de vy. Cette parallèle coupe la tangente. Cela donne la longueur du vecteur vitesse.
Si ce n'est pas suffisamment clair, je ferai un schéma...
Pas clair ==> "10 km/s-1 étant représenté par 005 cm"
005 cm ?... Il doit manquer une virgule, non ?
Désolé, j'ai été obligé de m'absenter...
Voilà un schéma qui expliquera ça mieux, je pense, mais c'est difficile à expliquer (et peut-être à comprendre 
)
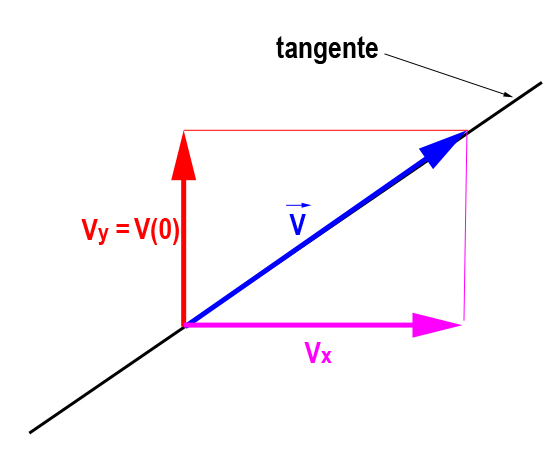
Et on a aussi la composante vx de la vitesse, ce qui sert dans les questions suivantes
Pour 3b et 3c, il faut faire cette construction : la tangente et le vecteur vy = v(0) (vertical vers le haut) aux points y= 3,0 cm et y = 5,0 cm.
Je ne peux pas le faire, le schéma que j'ai n'est pas assez précis et pas assez clair...
On demande aussi t5 - t3.
Comme y = v(0)t, on a : t5 - t3 = (y5 - y3) / v(0)
On peut déterminer vx en ces deux points comme il est expliqué dans le message précédent (en mesurant la composante vx sur le graphique avec l'échelle 0,5 cm pour 10 km.s-1).
Ceci nous permet de calculer l'accélération en y = 4,0 cm a4 = 
vx / t = (vx5 - vx3) /(t5 - t3)
Il reste la 3d mais il faut avoir "digérer" le reste avant...
Annuler
connectez vous