Inscription / Connexion Nouveau Sujet
La luge
Bonsoir !
Je suis actuellement sur un exercice de physiques et je ne parviens pas à répondre à la dernière question.
J'ai ainsi besoin d'aide s'il vous plaît.
Exercice : La luge
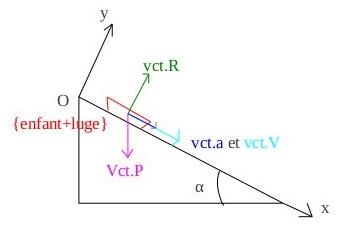
Le système {enfant+luge}, de masse m, dévale une piste faisant un angle α avec l'horizontale.
On néglige les frottements de l'air et de la piste.
1) Dans quel référentiel le mouvement est étudié ?
Le référentiel terrestre.
2) Quelle est la vitesse initiale du système ?
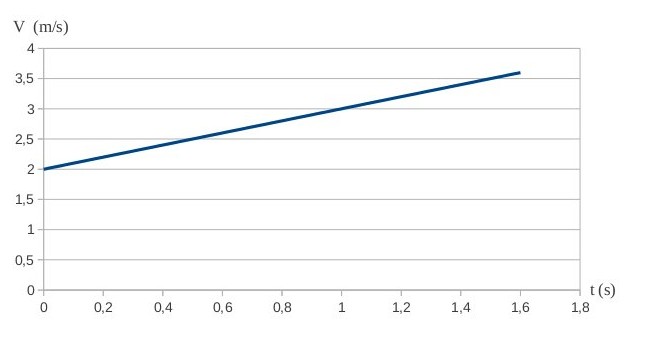
Par lecture graphique, la vitesse initiale vaut 2 m/s.
3)a) A l'aide de la courbe v=f(t), déterminer la valeur de l'accélération du centre d'inertie du système.
L'accélération est le coefficient directeur de la droite, soit a = 1 m/s
3)b) Quels sont le sens et la direction du vecteur 
?
est dans la même direction (du mouvement) et le même sens (trajectoire) que le vecteur 
.
4)a) Quelles sont les actions mécaniques qui s'exercent sur le système ?
Le poids, la réaction normale (et la poussée d'Archimède).
[/u]4)b) Représenter les forces modélisant ces actions sur un schéma.[/u]
===> schéma
5)a) Établir la relation vectorielle liant ces forces à l'accélération.
= m 
Soit 
+ 
= m*
5)b) En déduire la valeur de l'angle α.
C'est à cette question que je n'arrive pas à répondre
Salut 
,
(Je n'arrive pas à voir correctement les formules de 5a : les termes n'apparaissent pas à l'écran)
Mais je suppose que tu as appliqué le Principe Fondamental de la Physique (PFD) pour obtenir :
m*(Vct.a)=(Vct.P)+(Vct.R)=m*(Vct.g)+(Vct.R)
Or, tu as montré qu3b que (Vct.a) est de même sens et direction que (Vct.V) c'est-à-dire suivant l'axe(Ox).
Ainsi, si on projette le PFD sur les axes (Ox) et (Oy), on obtient :
m*a=m*g*sin(
)
0=-m*g*cos()+R
Delà, je pense que tu pourras facilement calculer avec une calculatrice (j'ai ~5,7°)
Sinon, le reste m'a l'air correct 
Merci d'avoir pris le temps d'y jeter un coup d'œil et pour les explications.
5)a) vect.F = m*vect.a
Soit vect.R + vect.P = m*vect.a
C'est ce que j'ai voulu écrire.
Pour la question 5)b), je suis désolée, je ne comprends toujours pas.
J'ai compris comment on trouve α mais pas la projection.
Salut,
Un vecteur, en particulier les vecteurs Vct.R , Vct.P , Vct.a , transmet 2 informations (dans la repère (xOy)): sa composante selon l'axe (Ox) et sa composante selon l'axe (Oy). Par projection, j'entends le fait d'isoler les composantes des vecteurs selon l'axe (Ox) de celles de l'axe (Oy).
Si on pose Vct.ex un vecteur unitaire parallèle à (Ox) et dans les sens des x croissants,
Vct.ey un vecteur unitaire parallèle à (Oy) et dans les sens des y croissants,
Zx ou Zy la composante d'un vecteur Z selon l'axe (Ox) ou (Oy)
On a :
(Vct.a)=(ax)*(Vct.ex)+(ay)*(Vct.ey)=a*(Vct.ex) car l'accélération est suivant (Ox)
(Vct.R)=(Rx)*(Vct.ex)+(Ry)*(Vct.ey)=R*(Vct.ey) car la réaction normale est suivant (Oy)
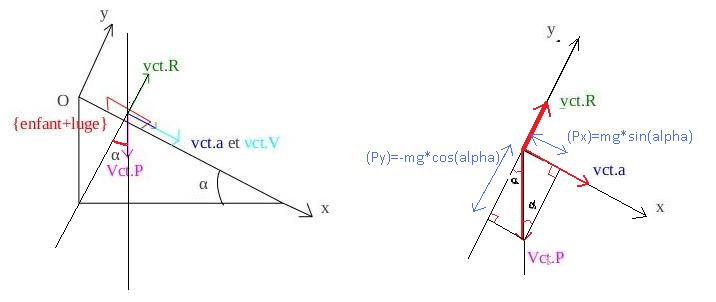
(Vct.P)=(Px)*(Vct.ex)+(Py)*(Vct.ey)=mgsin()*(Vct.ex)-mgcos()*(Vct.ey) , il faut utiliser la trigonométrie (cf schéma) dans les triangles schématisé.
Projeter un vecteur sur (Ox) revient à faire un produit scalaire entre lui et (Vct.ex), ainsi :
(ax)=(Vct.a).(Vct.ex)=(ax)*(Vct.ex).(Vct.ex)+(ay)*(Vct.ex).(Vct.ey)
avec (Vct.ex).(Vct.ex)=1 et (Vect.ex).(Vct.ey)=0 car (Vct.ex)
(Vect.ey)
On va projeter le PFD (l'équation vectorielle trouvée en 5a)) sur (Ox) et sur (Oy):
sur (Ox): m*(ax)=(Rx)+(Px) 
m*a=0+mgsin()
sur (Oy): m*(ay)=(Ry)+(Py) 0=R+mgcos()
Grace à l'équation obtenue par la projection sur (Ox), tu obtient l'expression de sin() en fonction de g et a connus, c'est gagné (avec une calculatrice)
J'espère que tu comprends mieux maintenant
Bonjour, j'ai le même exercice et j'en suis à la dernière question (5b et c), mais je suis bloquée car je ne vois pas comment calculer le vecteur(OP) puisque dans le cours on faisait en fonction du temps: Soit vecteur (OP) a pour coordonnees (x(t)= v0*cos alpha *t et y(t)= (-G*t²)/2+(vo*sin alpha)*t)
Mais je ne comprends pas quel t utilisé, comment as tu modéliser le vecteur P. Et comment en déduire la valur de l'angle puisque si t=0 alors tout s'annule...
Merci d'avance,
linceca05
Annuler
connectez vous