Bonjour à tous
J'ai un exercice merci beaucoup d'avance
Le stimulateur cardiaque est un dispositif électrique implanté dans le corps humain, qui active les muscles
relâchés dans le cœur du patient et lui donne l'énergie nécessaire à son fonctionnement. Afin d'éviter le
renouvellement du remplacement des piles électrochimiques, on utilise une pile particulier de plutonium ( ₉₄ ²³⁸ Pu)
radioactif type( ) sous forme d'un récipient hermétiquement fermé contenant une masse  m₀
de matières
radioactives.
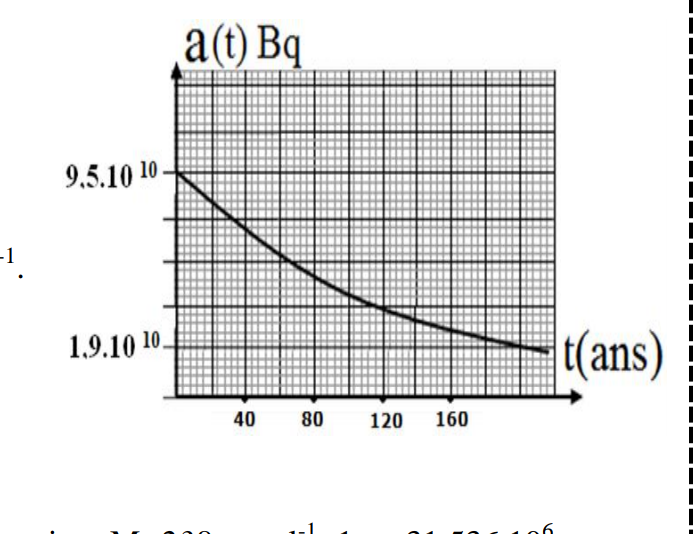
1)La courbe ci-contre donne l'activité a (t) de l'échantillon en
fonction de temps.
1.1) Déterminez l'activité initiale de l'échantillon utilisé.
1.2) Montrer que la constante de désintégration est = 2.5×10^-10 s^-1
1-3) Calculer N₀ le nombre de noyaux initiaux et en déduire la
valeur de la masse m₀ utilisée dans le stimulateur.
1-4) - On considère que le stimulateur fonctionne de façon
satisfaisante jusqu'à une diminution de 30 % de son activité.
A quel âge le patient doit-il remplacer le dispositif?
Données :
•Constante d'Avogadro
N_A=6,02*10²³ mol^-1
•Masse molaire de plutonium M=238 g.mol^-1
• 1an=31,536.10⁶ s

Mes réponses
1-1) graphiquement a₀=9,5*10¹⁰ Bq
1-2) On a
Et a(t1/2)=a₀/2
=9,5*10¹⁰/2=4,75*10¹⁰ Bq
Donc t1/2=87 ans =87*31,536*10⁶ s
•Donc
1-3) on sait que a(t)= ×N(t)
Donc a₀= N₀
Donc N₀=
Pour l'unité est ce que c'est ( bq.s)
Ensuite je ne sais pas franchement comment trouver m₀
la masse utilisé dans le stimulateur.
Une petite indications s'il vous plaît merci beaucoup d'avance