Bonjour,

Oui, c'est juste.

A est en m.s^-2 et B en kg^-1 ??
Parcontre après y'a une question je suppose qu'elle est mal formulée ou alors je ne la comprend pas:

2.2.6. Lorsque la vitesse de la bille atteint la vitesse limite vlim, trouver en justifiant, l'expression littérale de vlim en fonction de A et B. (0.5)


On dirait qu'il manque un bout de phrase non?

Merci d'avance pour vos réponse

Et pour la dernière question je n'y arrive pas non plus :

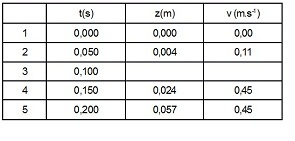
3.2. Le tableau donné en annexe (document 2) reproduit le début de la feuille de calculs du tableur déterminée par les expérimentateurs.

Les valeurs de la colonne t (s) représentent les dates de chaque image.

Les valeurs de la colonne z (m) représentent les ordonnées correspondantes du centre d'inertie.

Dans la colonne v (m.s-1), figurent les valeurs théoriques de la vitesse obtenues par la méthode d'EuIer.

À partir de l'équation différentielle, en utilisant la méthode itérative d'Euler, déterminer la valeur de v et de z à la date t = 0,100 s (écrire sur votre feuille le détail du calcul). (0.75)

Oui, A a la dimension d'une accélération

Non, la dimension de B est incorrecte.

Si tu ne veux pas "additionner des choux et des carottes" il faut que la dimension de B.v soit aussi celle d'une accélération.

Tu peux donc raisonner à partir de cette exigence. Tu peux aussi trouver facilement la dimension de k et en déduire celle de k/m

La question 2.2.6. me semble compréhensible sans rien avoir à y ajouter.

Mon message de 15 h 36 répond au tien de 15 h 08

Donc B = s^-1 ??

La méthode d'Euleur je ne l'es pas très bien comprise ... Parce que normalement dans le cours on a un tableau avc des formule qui contient le temps, la vitesse et l'accélération. or là on a le vecteur position et la vitesse et le temps ...
Et vous pourriez m'expliquer comment trouvé la valeur limitite svp ??

Merci d'avance

Oui la dimension de B est celle de l'inverse d'un temps.

Que vaut l'accélération quand la vitesse limite est atteinte ? Conséquence : quelle est l'expression littérale de cette vitesse limite ?

Quand la vitesse limite est atteinte l'accélération est nulle non ??

donc v lim= A/B

Exact !

Mais ce serait une meilleure idée de donner cette vitesse limite en fonction des paramètres du problème : g, , V, m et k

Oui oui pas de problème j'ai juste a remplaceer tout de façon ^^
Merci ^^

Et pour Euler?

Avec la méthode d'Euler on fait l'approximation que :
. la vitesse à l'instant t + t est la vitesse à l'instant t plus l'accélération à l'instant t que multiplie t
. la position à l'instant t + t est la position à l'instant t plus la vitesse à l'instant t que multiplie t

Quant à l'accélération tu la calcules à partir de l'expression dv/dt (elle dépend donc de v)

pour t = 0 s on a x = 0 m et v = 0 m.s^-1

Plus t est petit et meilleure est l'approximation.

Pour t=0 j'avais compris ... C'est pour n+1 que j'y arrive plus parce que comme je vous ai dis dans mon cours il n'y a que l'accélération la vitesse et le temps

Je ne comprends pas ta question.

Ici aussi tu as l'accélération (dont tu calcules une valeur connaissant la vitesse, c'est-à-dire la force de frottement), la vitesse et le temps. Tu peux ajouter la position connaissant vitesse et temps.

J'aurais aimé connaître tes résultats de la première partie. Quelle est la vitesse limite trouvée à cette première partie ?
Quelle accélération as-tu trouvée ?

Je comprends mal le tableau posté à 15 h 30
Si v = 0,45 m.s^-1 est la vitesse limite alors la position ne peut pas passer de 0,024 m à 0,057 m en 0,05 seconde

Ben c'est exactement celui qu'on me donne dans l'énoncé ...

A=1.4 et B=3.1 donc vlim=0.45 m.s^-1

Mais d'après le tableau c'est pas l'accélération qu'on a ... C'est la position, la vitesse et le temps c'est pas l'accélération ...

L'accélération c'est dv/dt

D'où viennent ces valeurs de A et B ? Comment les as-tu calculées ?

C'est une question 2.2.7. Calculer vlim sachant que A = 1,4 usi  et B = 3,1 usi .

Donc je me suis pas cassée la tête jai fait A/B donc 1.4/3.1

Désolé.

Je n'aurais pas dû te répondre. Tu n'as pas copié l'énoncé en entier. Il est impossible de t'aider correctement.

Un objet de masse m = 3,80 ^ 10-3 kg, de volume V = 2,10^10-6 m3 est lâché sans vitesse initiale dans un liquide de masse volumique = 1240 kg.m-3. Sa chute est filmée avec une webcam. Le film est ensuite numérisé puis analysé par un logiciel adapté. Le document fourni en annexe, montre l'ensemble des positions successives occupées par le centre d'inertie G de l'objet à intervalles de temps réguliers = 0,050 s.
Les frottements du fluide sur l'objet peuvent être modélisés par une force f opposée au vecteur vitesse et de valeur proportionnelle à la vitesse ; le coefficient de proportionnalité appelé coefficient de frottement sera noté k.
On prendra g = 9,8 m.s-2.

1. Le document fourni en annexe, montre que le mouvement de chute comporte deux phases de nature différente.
Préciser les natures de ces deux phases en précisant approximativement les positions limites de chacune d'elles. (0.5)

2. Étude de la première phase

2.1. À partir du document :

2.1.1. En tenant compte de l'échelle du document, calculer les vitesses en positions G3 et G5 puis tracer sur le document de l'annexe à rendre avec la copie, les vecteurs vitesses en ces positions en utilisant l'échelle 1 cm pour 0,20 m.s-1.  (0.75)


2.1.2. Calculer l'accélération a4 au point G4 puis tracer sur le document de l'annexe à rendre avec la copie, le vecteur accélération en ce point avec l'échelle 1 cm pour 0,50 m.s-2. (0.5)


2.2. Étude théorique

2.2.1. Calculer la valeur de la poussée d'Archimède A et montrer qu'elle est de l'ordre de grandeur du poids P.  (0.5)

2.2.2. Représenter les forces sur un schéma sans souci d'échelle. (0.25)

2.2.3. Énoncer la loi de Newton qui régit cette première phase. (0.25)

2.2.4. On pose : f = k . v
En appliquant la loi de Newton précédente, montrer que l'équation différentielle vérifiée par la vitesse v peut se mettre sous la forme :  
dv/dt + Bv = A              où A et B sont deux constantes
Donner les expressions littérales de A et de B en fonction de m, V, , g et k. (1)

2.2.5. Préciser les unités de A et B dans le système international. (0.5)

2.2.6. Lorsque la vitesse de la bille atteint la vitesse limite vlim, trouver en justifiant, l'expression littérale de vlim en fonction de A et B. (0.5)

2.2.7. Calculer vlim sachant que A = 1,4 usi  et B = 3,1 usi . (0.25)

3. Étude de la deuxième phase

3.1. Énoncer la loi de Newton qui régit cette phase. (0.25)

3.2. Le tableau donné en annexe (document 2) reproduit le début de la feuille de calculs du tableur déterminée par les expérimentateurs.

Les valeurs de la colonne t (s) représentent les dates de chaque image.

Les valeurs de la colonne z (m) représentent les ordonnées correspondantes du centre d'inertie.

Dans la colonne v (m.s-1), figurent les valeurs théoriques de la vitesse obtenues par la méthode d'EuIer.

À partir de l'équation différentielle, en utilisant la méthode itérative d'Euler, déterminer la valeur de v et de z à la date t = 0,100 s (écrire sur votre feuille le détail du calcul). (0.75)

(Pour le tableau voir post 15:30)

voilà là l'énoncé il est entier !