Bonjour
Soit la différence des distance du point M aux deux sources :
Si =k. (k entier relatif) : interférence constructive ;
Si =k.+/2 interférence destructive.

oui  mais il n'y a pas de calcul à faire seulement la representation de  l'allure  
de plus si je mesure c'est à peu prés ?

bonjour je reviens pour ma question comment sans faire de calcul (juste avec le "schéma") on peut déterminer si les ondes qui arrivent  en  M et M' sont  constructives ou destructives  ?
est-ce parce que M est plus prés de la source que M' ??

2 autres questions :
la difference de marche peut-elle être negative ?

quelles sont les conséquences des interférences ?
s'il y a interférences un phénomène ondulatoire se produit, les ondes se rencontrent



merci

personne pour me guider ???

Dans ma première réponse : k est un entier relatif c'est à dire un entier positif ou négatif. peut donc être négatif.
J'imagines que les cercles tracés de centres confondus avec les deux sources ont des rayons qui s'expriment simplement en fonction de la longueur d'onde (rayons sans doutes multiples de /2.
Tu peux donc graphiquement exprimer en fonction de et prévoir si, à l'intersection de deux cercles, les interférences sont constructives ou destructives.
Si mes explications ne te paraissent pas suffisantes, scanne ton document et poste le ici. Cela me permettra d'être plus précis dans mes explications.

énoncé :  représenter l'allure au point M en fonction du temps puis en M'
(la qualité n'est pas très bonne donc on ne boit pas bien les "cercles" / ondes qui se croisent)

merci

Le schéma ci-dessous devrait t'aider.
Tu peux graphiquement mesurer la longueur d'onde . Tu peux aussi mesurer la différence de marche =d2-d1 Reste ensuite à voir, aux approximations de mesures près, si tu te trouves dans un des deux cas particuliers déjà évoqués. Faire la même étude pour le point M.

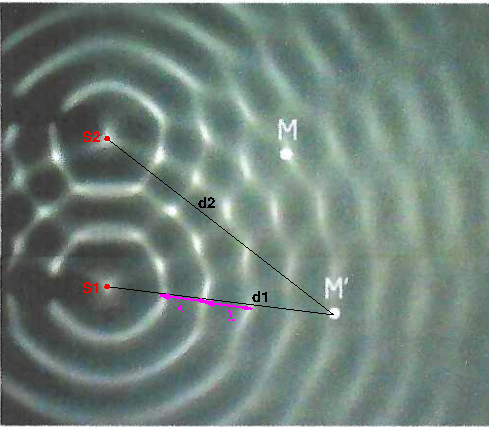
alors cela ferait
pour M d2-d1 = 6-5 = 1  
(d1 est a  5 et d2 à 6) donc 1 est nombre entier = interference constructive
pour M' d2-d1 = 4-5 = -1
(d1 est à 5 et d2 à 4) là je ne sais pas quand c'est négatif

(je précise que cet exercice est corrigé dans mon livre et il n'y pas de calcul juste ..au point M les interférences sont constructives ..puis la représentation ?)  

d2-d1=6-5= (pas 1 !)
J'ai choisi arbitrairement S1 et S2 : il serait possible de permuter et on obtiendrait =- pour M' et pour M. Ce qui compte c'est la conclusion : quels que soient les indices attribuées au deux sources : les interférences sont constructives dans les deux cas.

le problème c'est que dans la correction en M elles sont constructives et en M' destructives ils font l'allure du signal mais ils n'expliquent rien !!

Tu dis que ton corrigé indique = pour un point et =- pour l'autre ; je n'ai pas vérifié ; tu peux le faire : je t'ai indiqué la méthode sur le document scanné. S'il n'y a pas d'erreur sur la détermination des différences de marche : il y a bien interférence constructive dans les deux cas. Comme déjà dit, il y a interférence destructive si :
=k.+/2

non voici l'énoncé :
des interférences à la surface de l'eau dues à la superposition de 2 ondes sinusoïdales issues de 2 sources ponctuelles synchrones émettant en phase sont observées
représenter l'allure du signal au point M en fonction du temps puis au pont M'
et le corrigé commence par : au point M les interférences sont constructives ..
puis il y a l'allure
dans mon post de 16:00 j'ai proposé un calcul suite à votre post !!

J'ai agrandi la figure et essayé de faire des mesures plus précises... On obtient bien en M' :
S1M'=d1=5 et S2M'=6. Les deux ondes arrivent en phase en M' ; il y a interférence constructive ; l'amplitude des oscillations y est maximale.

ok il y a déjà eu des corrections fausses
donc les ondes sont constructives en M et M'

mais comment décide-t-on qui est S1 S2 d1 d2 ??
car les résultats ne sont pas le mêmes

Bien sûr que non ! Crois-tu vraiment que le fait de permuter les indices 1 et 2 sur un dessin puisse modifier le phénomène d'interférence ?
Si =k. avec k entier relatif, il y a interférences constructives. Cela est vrai pour k=1 mais vrai aussi pour k=-1. Si ton corrigé affirme le contraire, il se trompe.

désolée je ne comprends pas !
sur la représentation vous avez noté d1 = 5 et d2 6 donc d2-d1 = 6-5 = 1 d'accord mais comment on choisit qui est d1 et d2 ??
c'est ça que je ne comprends pas car si on inverse d1=6 et d2 = 5 d2-d1 = 5-6 = -1 ?

As-tu compris ce qu'on appelle en math un nombre entier relatif ?

oui mais dans un autre exercice de meme type on trouve k=-2 et la conclusion c'est que les ondes sont destructives !

Si =k.+/2 avec k=-2 : tu as bien des interférences destructives.
Si Si =k. avec k=-2 : tu as bien des interférences constructives.
Je suppose bien sûr que, comme dans cet exercice, les deux sources vibrent en phase. Il faudrait inverser les résultats si les sources vibraient en opposition de hase.

d'accord
on calcule la longueur d'ondes puis d2-d1 on trouve k
mais ici je ne connais pas f
donc comment connaitre la longueur d'ondes

Je te l'ai indiqué sur le schéma : c'est la distance entre deux"rides " circulaires successives. Revois dans ton cours la définition de la longueur d'onde.

ok merci !