Inscription / Connexion Nouveau Sujet
interaction gravitationnelle
Bonjour
Le professeur demande a ton groupe de travail de déterminer la masse de Jupiter en étudiant le mouvement de ses principaux satellites : lO, Europe,Ganymède et Callisto .
L étude du mouvement de ces satellites s effectue dans un repère considéré comme galiléen, ayant son origine au centre de la planète et ses axes dirigés vers des étoiles lointaines ,considerons comme fixe . Jupiter et ses satellites
[url][/url] sont supposés a répartition de masse a symétrie
Sphère
Le saTellite de masse m,se deplace sur une trajectoire circulaire, distance R du centre de Jupiter
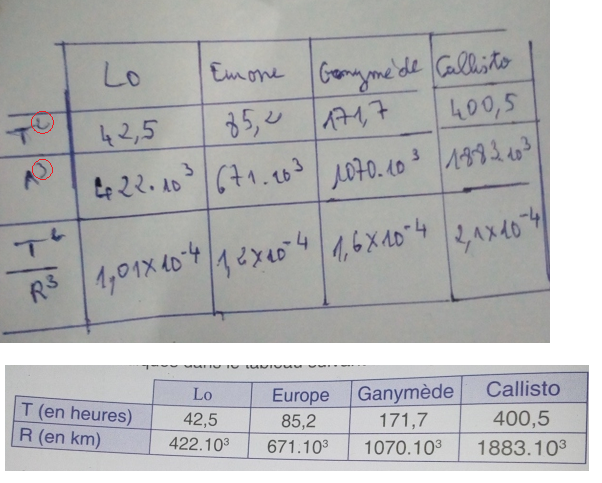
Les periodescde révolutions et les rayons des orbites des quatres principaux satellites de Jupiter sont indiqués dans le tableau suivant.
Données échelles : abscisses :1cm représente 10^11 s^2
Ordonnées 1 cm représente 4,10^26 m^3
1. Force d interaction gravitationnelle
1/1 donne l expression de la force d interaction gravitationnelle exercée par Jupiter sur son satellite
1/2 représente sur un schéma cette force
2/Étude du mouvement.
2/1 montre que le mouvement du satellite est circulaire et uniforme
2/2 déduis de ce qui précède l expression de la période de révolution T du satellite .
2/3 montre que le rapport T^2/R^3 est constant
3/ masse de Jupiter
3/1 représente sur un papier millimètre ,le graphe donnant les variations de T^2 en fonction de R^2
3/2 établi la relation entre T^2 et R^3
3/3 déterminer la masse M de Jupiter
repaetit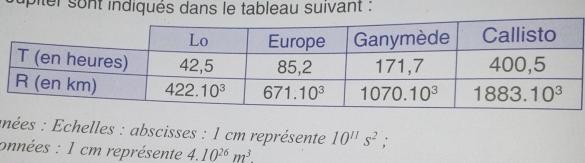
***Image recadrée***
Question 1
F=G*MJ*ms/(RJ+Z)^2
MJ désigné la masse de Jupiter
ms masse du satellite
Question 2
J aimerais savoir si je dois tenir compte du tableau pour représente F
Bonsoir,
Question 1 :
Que représente ton " Z " ?
Question 2 :
Non, tu représentes Jupiter, son satellite, et la force demandée sans souci d'échelle.
D'ailleurs, il n'est pas précisé ici lequel des satellites est concerné.
Laisse moi rigoler .... 
Si c'était une faute de frappe tu n'aurais pas répondu dans un premier temps que " h " était "la hauteur "
J'ai compris que G était la constante universelle de gravitation, que MJ était la masse de Jupiter et FJ/S l'intensité de la force exercée par Jupiter sur le satellite.
L'énoncé impose de désigner la masse du satellite par la lettre " m "
Merci de ne pas modifier cette notation et de définir toutes celles que tu crées.
L'expression cherchée est alors : FJ/S = G * MJ * m / R²
J ai une question concernant la représentation de la force
Comment retrouver sa valeur
Comme je te l'ai déjà dit (mais lis tu mes réponses ?) tu n'as pas à te soucier de l'intensité de cette force pour la représenter
Ton schéma doit représenter Jupiter, son satellite, le vecteur représentant la force demandée (correctement dirigé, correctement orienté)
Tu donnes à ce vecteur la longueur que tu veux.
Question 2/1
Projection dans (Z,n)
Vecteur a( DV/dT=0 (1),V^2/r=g (2)
(1) => V=cst le mouvement du satellite est uniforme
2 V^2/R=g =Gms/R^2=>R=G*mes/v^2
R=cst donc Le mouvement du satellite est circulaire
D ou le mouvement du satellite est circulaire et uniforme
Question 2/1
Ton calcul est peut être bon (ou pas):
Il n'est jamais justifié.
En tout cas, il est trop confus pour moi : Je renonce à le comprendre.
Je propose une solution qui ne nécessite aucun calcul :
L'énoncé dit :
Le satellite de masse m, se déplace sur une trajectoire circulaire, distante de R du centre de Jupiter
Le mouvement du satellite est donc circulaire.
La seule force qui s'exerce sur le satellite est la force de gravitation qui ne travaille pas car constamment perpendiculaire au déplacement.
En appliquant le théorème de l'énergie cinétique on en déduit que cette énergie ne varie pas et par suite que la vitesse ne varie pas non plus.
Le mouvement du satellite est donc uniforme.
Question 2/2
Ca démarre bien mal :
T qui est une durée ne peut pas être égal à 2π/V qui est l'inverse d'une vitesse.
N'importe comment tu réponds ici à une question qui est la question 3.2 et ce n'est pas ce qu'on te demande.
L'énoncé précise de déduire de ce qui précède l'expression de la période de révolution T du satellite .
Il te faut trouver une relation entre T et R ( et non r !!! ) dans laquelle il n'y a ni G, ni m ( et non ms !!! )
Question 1/2
Oui, la représentation est exacte.
Question 2/2
Utilise la définition générale de la vitesse appliquée à une distance parcourue par le satellite égale au périmètre de son orbite.
Non.
Un peu lassant de répéter toujours les mêmes choses :
a) Tu n'as pas défini ce qu'est " d " , je suppose que c'est une longueur mais laquelle ?
b) Ton résultat n'est pas justifié.
c) Ce résultat est très vraisemblablement faux car si " d " représente une longueur, alors V qui est probablement une vitesse ne peut pas être égale à une longueur.
d) On cherche une relation entre V, T, et R et je ne vois dans ton résultat ni T, ni R
Donc, tu sais (heureusement !) calculer le périmètre d'un cercle !
Mais le périmètre est une longueur, pas une vitesse.
Alors pourquoi écris tu que V (la vitesse) est égal à 2πR qui est une longueur ?
Et que devient " T " dans cette histoire ?
Évidemment puisque cette expression dit qu'une vitesse est égale à une longueur !
Au fait quelle est la définition de la vitesse ?
Et bien puisque tu sais ce qu'est une vitesse pourquoi ne t'en sers tu pas pour répondre à la question posée ?
Distance parcourue ............. ? .............
Durée pour parcourir cette distance ............. ? .............
Vitesse ............. ? .............
Tu auras alors, comme prévu, une relation entre V, R, et T
V = d/T ..... D'accord !
Mais V = 2πR est une énorme erreur que tu as déjà commise et que je t'ai déjà signalée !
 Ouf
Ouf 
C'est exact !
Avec :
R : Rayon de l'orbite circulaire du satellite
T : Période du satellite ( durée nécessaire pour faire le tour de Jupiter )
V : Vitesse (constante) du satellite
Question 2/3
J aimerais savoir si je dois utiliser le tableau pour montrer que le rapport est constant
Question 2/3
V^2/R=g=G*m/R^2=> V^2=G*m/R..ou T=2pi/V => v=2pi R/T
V^2=4piR^2/T^2=G*m/R
=> R^3/T^2=G*m/4Pi^2=Cst
Question 2.3
Voilà déjà 2 fois que tu réponds à la question 3/2 au lieu de répondre à la question qui t'es posée.
Patience, on va y arriver à cette démonstration, mais ce n'est pas ce qu'on te demande ici.
Utilise le tableau pour montrer que pour les 4 satellites le rapport T²/R³ est constant.
Tes résultats sont faux ( au moins en partie)
Tu dois bien t'en douter puisque on s'attend à trouver que le rapport T²/R³ soit le même pour les 4 satellites ce qui n'est pas du tout ce que tu obtiens.
Pourquoi as tu "oublié" Ganymède ?
Remarque :
Pour cette question tu peux tout à fait conserver les unités de l'énoncé ( heures et kilomètres ). Tu obtiendras T²/R³ en h²/km³.
En effet si T²/R³ est constant en h²/km³ il le sera aussi en s²/m³