Inscription / Connexion Nouveau Sujet
induction limite d'une vitesse
Bonjour. Je m'entrainais encore sur les exercices de physiques quand je suis tombé sur une question que je n'arrivais pas réellement à faire dans mon exo concernant la limite de la vitesse d'une barre.
Voici l'énoncée
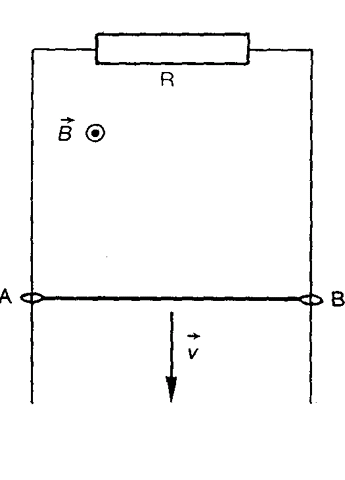
Une barre AB horizontale de masse m et de longueur l, de résistance négligeable est lâchée sans vitesse à l'instant initial t=0. Elle tombe en restant parallèle à elle même dans une région de l'espace ou règne un champ magnétique uniforme B Horizontal et perpendiculaire à la barre. La chute de la barre est guidée par deux fils verticaux conducteurs de résistance négligeable
on suppose que les forces de frottements sont nulles. B=0.5T
1- Donner l'expression de la f.é.m. induite e qui apparaît en fonction de B , l et v
*Pas de problème pour ça:
e=-d /dt
/dt
d =B
=B S=B*l*dL
S=B*l*dL
dL=Vdt
donc d =Blvdt
=Blvdt
d'où  =Blvt
=Blvt
donc e=-Blv
2-) donner l'expression du courant induit
i=e/R
i=(-Blv)/R
3-*la question me posant problème*; Appliquer le théorème du centre d'inertie à la tige puis montrer que la tige atteint une vitesse limite en fonction de B,l,g et R. Calculer V limite
Je prend le schéma dans quelques instants..
Merci d'avance.
Bonjour
Tu t'es déjà bien débrouillé !
Pour la suite : pense à la loi de Laplace : La tige parcourue par le courant induit et placée dans le champ magnétique est soumise à une telle force qui, selon la loi de Lenz, sera nécessairement une force résistante, donc une force orientée vers le haut. Elle va dépendre de la vitesse.
Applique ensuite le théorème du centre d'inertie. Tu vas obtenir une équation différentielle du premier ordre vérifiée par la vitesse. La vitesse limite sera obtenue lorsque la force de Laplace compensera exactement le poids...
Je te laisse réfléchir à cela et proposer seul une solution...
Merci de me venir en aide!
J'ai donc suivi votre conseil.
TCI :  (F)=ma
(F)=ma
-F+P=ma
mg-F=ma
a=g-IBl/m
or I=(-Blv)/R
donc a=g+[(B^2)*(L^2)*v]/Rm
donc la force de Laplace compense le poids : d'où g+ [(B^2)*(L^2)*v]/Rm=0?
Tu as juste commis une erreur de signe. Si tu laisses F en mesure algébrique (donc ici F<0) le TCI conduit à : F+P=ma
A t=0, v=0 donc a = g : la tige accélère comme en chute libre mais, au fur et à mesure que la vitesse augmente, la force de résistance augmente. Au bout d'un certain temps, cette force de Laplace compensera pratiquement le poids, l'accélération sera alors pratiquement nulle et la vitesse constante. Ce cas limite correspond donc à a=0. Raisonne à partir de la première relation ci-dessus ou de la seconde : tu arrives dans les deux cas à la même vitesse limite :