Inscription / Connexion Nouveau Sujet
Incompréhension sur la relativité restreinte
Bonjour, je ne comprends pas un détail de ce paragraphe :
" Lorsque deux horloges sont en mouvement relatif, on observe une dilatation des durées. L'horloge en mouvement par rapport au référentiel de l'observateur <<bat>> plus lentement."
Ainsi pour un même évènement , l'horloge qui est dans un référentiel galiléen proche de l'évènement montre un durée écoulée moins importante(temps propre) que l'horloge qui est dans un référentiel galiléen éloignée du lieu de l'évènement et en mouvement(temps mesurée)
avec temps mesurée = gamma * temps propre . Or si j'en crois ce paragraphe cité plus haut , si l'horloge "bat" plus lentement , cela voudrait donc dire que la durée écoulée que montrerait l'horloge éloignée de l'évènement serait inférieur à celle de l'horloge proche de l'évènement car une seconde durerait moins longtemps dans l'horloge éloignée de l'évènement que l'horloge proche de l'évènement . Ce que je veux dire c'est que si l'horloge bat plus lentement , cela veut dire qu'au lieu d'avoir Tic .. tac .. tic .. tac à chaque seconde , on aurait tic ....... tac.......tic.......tac et donc pour une même durée , l'horloge éloignée de l'évènement afficherait une date inférieur à celle proche de l'évènement . Or comme d'après le cours je sais que l'horloge éloignée montre la durée mesurée qui est supérieur à la durée propre , j'ai plutôt l'impression que l'horloge bat plus vite et donc qu'on a tic tac tic tac tic tac et donc cela me semblerait plus logique que la durée mesurée soit supérieur à la durée propre ici ...
Je pense avoir compris la totalité du chapitre de la relativité restreinte mais ce détail que je ne comprends pas me gêne . Pourriez vous m'expliquer précisément et de la manière la plus développée possible pourquoi on dit que l'horloge "bat plus rapidement" car cela me semble contradictoire avec le fait que la durée mesurée est plus grande que la durée propre ...(j'ai plutôt l'impression que l'horloge éloignée de l'évènement bat plus vite puisque durée mesurée > durée propre)
Merci d'avance .
Bonjour,
Eh bien, ni l'un ni l'autre...
Si les deux horloges sont identiques, elle battent tout simplement exactement au même rythme pour des observateurs placés à côté d'elles.
Mais chaque observateur voit les horloges de l'autre battre plus lentement que la sienne (celle à côté de laquelle il se trouve).

D'accord mais dans "Mais chaque observateur voit les horloges de l'autre battre plus lentement que la sienne (celle à côté de laquelle il se trouve).
" je ne comprends toujours pas pourquoi on dit "battre plus lentement" et non pas "battre plus rapidement" ...
Je trouve dommage, mais c'est ainsi, que l'initiation à la relativité restreinte en terminale ne soit pas accompagnée par quelques tracés de diagrammes de Minkowski ou de Loedel.
Voici un diagramme de Loedel qui illustre ma réponse :
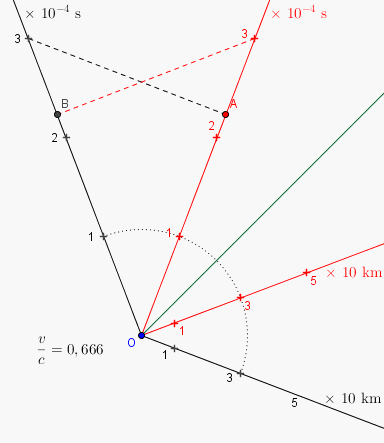
Un observateur utilise le référentiel noir, l'autre le référentiel rouge.
Ces deux référentiels sont en mouvement relatif avec v / c = 2 /3
et donc 
 1,342
1,342
Au moment où un observateur voit une durée de 3.10-4 seconde sur son horloge propre (celle qui est placée à côté de lui) depuis l'événement où ils étaient côte à côte (point O) chacun peut lire que l'horloge de l'autre ne marque qu'environ 2,236.10-4 seconde

L'horloge qui est à côté de moi vient de terminer son troisième battement (un battement tous les 10-4 seconde) et va commencer son quatrième.
Je vois l'horloge de l'autre qui vient juste de commencer son troisième battement : elle bat donc plus lentement !

Merci pour cette explication qui me fait mieux comprendre l'expression "bat plus lentement" mais alors, si lorsqu'on a 3.10^-4 seconde sur son horloge propre , on a 2,236.10^-4 seconde sur l'autre horloge alors comment cela se fait-il que , à la fin de l'évènement produit près de l'horloge propre, l'horloge propre montre une date inférieure à celle de l'autre horloge ... ? Si je suis ce que vous venez d'écrire j'ai plutôt l'impression que c'est l'horloge propre qui montre une date supérieure à celle de l'horloge éloignée .
Il n'y a pas UNE horloge propre.
Dans chacun des deux référentiels, chaque observateur a près de lui une horloge qui est son horloge propre.
Tu as raison d'introduire le concept d'événement.
Soit la durée entre les deux événements O et A
O : les deux observateurs, chacun est immobile dans son référentiel qui est en mouvement par rapport à l'autre, sont côte à côte. Leurs horloges, bien synchronisées, marquent toutes les deux zéro.
A : l'observateur dans le référentiel rouge voit son horloge marquer 2,236.10-4 s
L'observateur du référentiel noir lit sur son horloge 3.10-4 s lors de l'événement A
"Rouge" conclut que la durée entre O et A est de 2,236.10-4 s
"Noir" conclut que cette durée vaut 3.10-4 s
Mais...
La seule horloge présente à la fois en O et en A est l'horloge rouge. C'est elle qui indique donc un temps propre, alors que les horloges de "Noir" indiquent un temps mesuré plus long (pour "Noir" ce n'est pas la même horloge qui se trouve à l'emplacement de l'événement O que celle qui se trouve à l'emplacement de l'événement A)
Et réciproquement...
Soit la durée entre les deux événements O et B
O : les deux observateurs, chacun est immobile dans son référentiel qui est en mouvement par rapport à l'autre, sont côte à côte. Leurs horloges, bien synchronisées, marquent toutes les deux zéro.
B : l'observateur dans le référentiel noir voit son horloge marquer 2,236.10-4 s
L'observateur du référentiel rouge lit sur son horloge 3.10-4 s lors de l'événement B
"Noir" conclut que la durée entre O et B est de 2,236.10-4 s
"Rouge" conclut que cette durée vaut 3.10-4 s
Mais...
La seule horloge présente à la fois en O et en B est l'horloge noire. C'est elle qui indique donc un temps propre, alors que les horloges de "Rouge" indiquent un temps mesuré plus long (pour "Rouge" ce n'est pas la même horloge qui se trouve à l'emplacement de l'événement O que celle qui se trouve à l'emplacement de l'événement B)



