Inscription / Connexion Nouveau Sujet
Grand oral
Bonjour, pour mon grand oral mon sujet est " Quelle doit être l'intensité de la force nécessaire pour dévier un astéroïde ?". Cependant, j'ai du mal a débuter mes calculs pour trouver l'intensité nécessaire en sachant que je veut le dévier d'une distance précise par rapport à la Terre. Si quelqu'un pourrait m'expliquer les démarches ca serait sympa .
Bonsoir,
C'est une question intéressante mais pas simple à traiter pour un Terminale, à mon avis :
Il faut déjà bien poser le problème que tu veux traiter:
- faire un croquis avec la Terre et l'astéroide
- préciser les conditions initiales (direction, vitesse, ...)
- expliquer et représenter la trajectoire de l 'astéroide (si on ne fait rien)
- préciser les paramètres de cette trajectoire sur lesquels on peut agir
- préciser ce qu'on entend exactement par "dévier" l'astéroide
et alors seulement on pourra peut-etre tenter un calcul....
Bonsoir ,
D'abord merci pour ta réponse et pour toutes les conditions j'ai déjà essayer de les posé a l'aide des conseils de mon profs et les voici:
-En premier lieu je me place dans un référentiel géocentrique
-ensuite je dit que l'astéroïde et rectiligne par rapport à la terre
après j'avoue que je ne sais pas si je doit établir une vitesse initial étant donné que le fait de trouver la force nécessaire et déjà compliqué( même mon prof à trouver ce sujet dur à traiter). Cependant j'ai essayer de de faire un croquis avec lui sur le but de l'exos qui serait de tracer une trajectoire à l'astéroïde en inventant un axe pour que cela ressemble à un exo classique de Meca .
Du coup à partir de cela auriez vous des idées sur comment je peut entreprendre mon exercice .
Merci d'avance, Bonne soirée et voici le croquis ci dessous
Pour simplifier, effectivement, on peut se placer dans le ref. geocentrique (meme si pour faire le vrai calcul il faut se placer dans le ref. heliocentrique pour un tel probleme, car le soleil intervient , et le cas echeant d'autres planetes aussi! )
Peux-tu poster ton croquis, que je vois mieux la situation physique que tu voudrais traiter?
-ensuite je dit que l'astéroïde est rectiligne par rapport à la terre
Que veux-tu dire?
Bonjour,
Tu avances avec tes asteroides?
Est-ce que tu pensais traiter la situation suivante? (Cf schema)
A: asteroide
T: centre de la terre
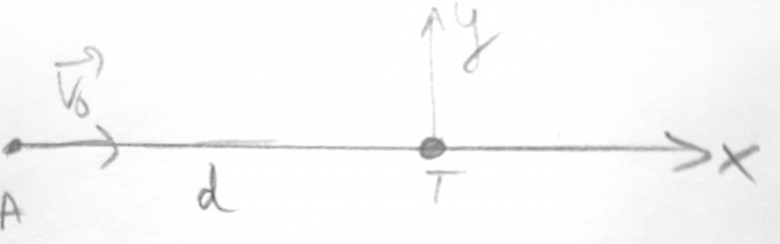
Bonjour,
voici le schéma que j'ai établi avec mon prof et l'idée serait de déplacer l'astéroïde dans le mouvement des pointillées ( avec des proportions bien précise). En revanche je ne sais pas comment introduire la vitesse de l'astéroïde.
Merci d'avance
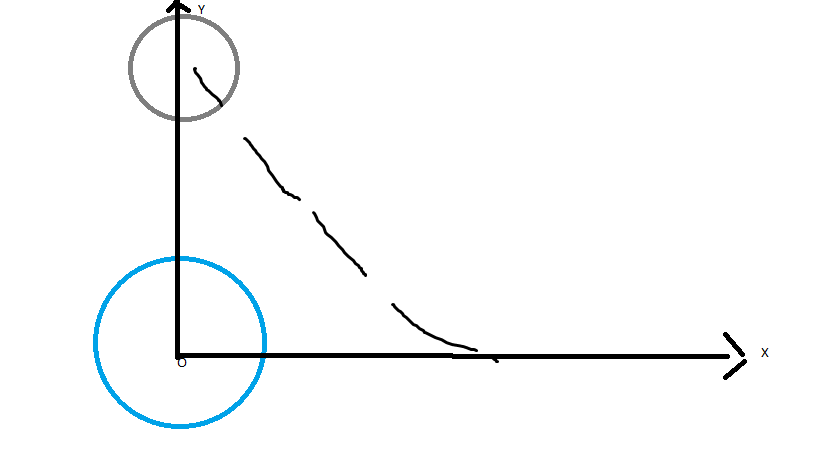
donc j'avais deviné (à une rotation près)
C'est la situation la pire qui soit puisque l'astéroide (A) fonce droit sur la terre! (très très peu probable, heureusement)
L'étape suivante est de faire un schéma avec la vitesse initiale de A et d'expliquer qu'il faut détourner A, càd physiquement modifier sa vitesse  o. Et pour cela on peut effectivement lui appliquer une force pour que sa vitesse varie de
o. Et pour cela on peut effectivement lui appliquer une force pour que sa vitesse varie de 
 , voir croquis.
, voir croquis.
La NASA a déjà testé cela en envoyant une sonde s'écraser avec une grande vitesse sur un astéroide.
La question suivante est donc: que vaut b = TH en fonction de d,  v et Vo ?
v et Vo ?
(on va supposer  "petit" car d >> b ici, je pense)
"petit" car d >> b ici, je pense)
(b s'appelle le paramètre d'impact)
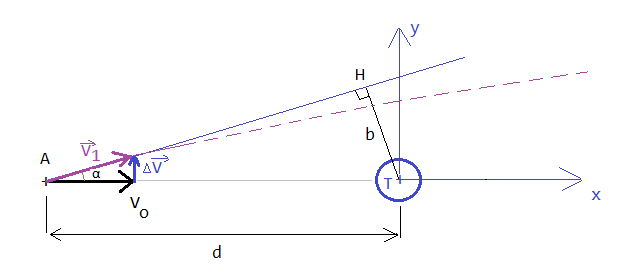
Bonjour,
Du coup j?ai essayer de mettre b en fonction du reste mais je suis bloqué parce que je me retrouve toujours avec b en fonction de b aussi . Je voulais passez par le cosinus mais j?ai vu sur internet que lorsque l?angle a est petit cos(a) ~1 donc comment faire ( je mais l?image ci dessous)
----------
***Edit gbm : attention, les pistes de réflexion doivent être recopiées ! Tu as tous les utilitaires nécessaires pour y parvenir (éditeur de symboles et LATEX)***
Ah bah tout simplement , puisque tan(α)=ΔV/V0 et sin(α)=b/d et que α est très petit donc tan(α) et sin(α)~=α donc :
ΔV/V0=b/d et on a bien:
b=ΔV/V0*d
Merci , maintenant ou dois je en venir avec toutes ces données ? ( et merci de prendre le temps de me répondre ca me fait plaisir)
C'est ca!
Donc si on fixe Vo, b et d , on trouve  v et on peut en deduire l'impulsion qu'il va falloir communiquer à A pour le devier.
v et on peut en deduire l'impulsion qu'il va falloir communiquer à A pour le devier.
Il y a toutefois un hic car A n'a pas une trajectoire rectiligne. Et b n'est pas la distance minimale entre A et T.
Sais-tu le type de trajectoire que suit A apres qu'on l'ait devié ? (et representee en pointilles sur mon dessin)
Eh bien l'idée serait de l'aterrir a peu près ici( vers le point H ) avec une vrai donée (8 000 000km ) car c'est à cette distance qu'un asteroïde n'est plus dangereux pour la terre. Mais est ce que avec tout ces "hics" mon devoir reste jouable ?
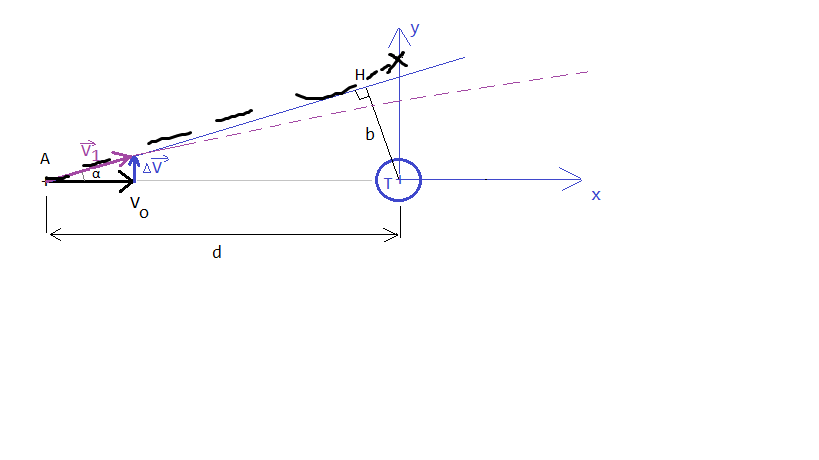
on n'a pas besoin de prendre b aussi grand pour eviter une catastrophe, b=50.000 km suffirait largement, peut-etre meme moins.
Le rayon terrestre est de 6400 km et si on ajoute l'atmosphere, ca fait 6600 km.
Et si on veut preserver nos satellites, il faut alors ajouter encore 36000 km (orbites geostationnaires)
Je voulais juste faire remarquer que si on choisit b=50000 km par ex. , en fait A va passer à moins de 50000km de la terre car A est attiré par la terre et dévié (la vraie trajectoire est une branche d'hyperbole) . Mais c'est hors programme, donc on va negliger cette deviation, ici, et prendre b "assez grand" .
L'etape suivante est de calculer la force que doit subir A pour que sa vitesse varie de 
 , mais ca, c'est presque une question de cours.
, mais ca, c'est presque une question de cours.
Donc si je comprend bien , en fixant des valeurs précise pour b,d,et V0 , il me suffirai seulement de calculer ΔV pour ensuite trouver l'accélération et trouver la force , mais je n'ai pas de temps requis dans mon exercices
Oui, puisque F M
M  V/
V/ t
t
où M est la masse de A
Ici on a un choc entre une sonde (un impacteur) et A, donc il faut evaluer  t, à 1s peut etre?
t, à 1s peut etre?
En fait la force n'est pas le bon parametre, c'est l'impulsion M 
 qui compte et il y a une relation entre M
qui compte et il y a une relation entre M 
 , la masse m de l'impacteur et sa vitesse
, la masse m de l'impacteur et sa vitesse  par rapport à A au moment de l'impact. Mais c'est un choc mou, je ne sais pas si tu sais traiter ca...
par rapport à A au moment de l'impact. Mais c'est un choc mou, je ne sais pas si tu sais traiter ca...
Non , le choc mou n'est pas au programme de terminale ...
Mais je n'est pas compris qu'est ce qui durerai 1sec le choc ? Je suis perdue sur cette question de temps
reprenons:
un astéroide A doit être dévié de sa trajectoire. Une des solutions est d'envoyer une sonde (un impacteur) le percuter à grande vitesse et donc de provoquer un choc qui va changer la vitesse de A de 

Mais comme tu ne sais pas traiter les chocs, et que tu voudrais plutôt évaluer la force à exercer sur A, nous sommes obligés d'utiliser la 2e loi de Newton directement et d'évaluer la durée du choc : 1s ou 2s par ex. (ca va très vite et c'est très violent car l' impacteur a une vitesse  de plusieurs km/s (par rapport à A) au moment de l'impact!
de plusieurs km/s (par rapport à A) au moment de l'impact!
Ca va te donner une force gigantesque...
Tu peux prendre pour valeurs, pour voir:
masse de A: M = 50 109 kg
Vo = 5 km/s (dans le ref. geocentrique)
b = 50000 km
et d de plusieurs millions de km, sachant que plus A est loin, plus c'est facile de le dévier.
En prenant d=1 000 000 km pour d je trouve 2,5e16 N pour la force (j'ai laisser en tonne. est ec que c'est bon? et est ce que je peut commencer à rediger avec toutes ces infos?
il vaut mieux tout exprimer en USI, le calcul approché donne:
F 
avec
masse de A: M = 50 109 kg
Vo = 5 km/s (dans le ref. geocentrique)
b = 50000 km
 t
t  1 s
1 s
d = 106 km
je trouve:
F  1013N
1013N
(on ne retient que l'ordre de grandeur, ici, vu le calcul très approché)
Il faudrait énormément d'impacteurs pour obtenir ca, ce qui rend la solution irréaliste aujourd'hui.
Une solution pour faire baisser F est d'augmenter fortement d, c'est à dire d'intervenir bcp plus tôt. Mais pour les astéroides qui proviennent de la ceinture d'asteroides entre Mars et Jupiter, d ne peut guère excéder 100 millions, donc on gagnerait un facteur de l'ordre de 100 tout au plus.
Remarque: en fait, on a oublié une force dans le bilan lors du choc, il aurait fallu écrire:
+ .....
 M
M
sais-tu laquelle et peux-tu montrer qu'elle est négligeable ?
C'est la force gravitationelle mais face à un ordre de grandeur tel que e13 elle est negligeable n'est ce pas ?
il vaut mieux le vérifier qd meme, A n'est pas un petit caillou  , sa masse est énorme par rapport aux objects usuels.
, sa masse est énorme par rapport aux objects usuels.
Et encore, il y a des astéroides bcp plus massifs...
Don quest ce qui serait ideal pour moi maintenant je compte la force gravitationelle et après la force nécessaire sera facilement trouvable ?
non, tu appliques la 2e loi (approchée) de Newton à A lors du choc:
+
 M
M
tu calcules P avec la loi de la gravitation universelle
tu calcules M  V /
V /  t
t
et tu remarques que P << M  V /
V /  t,
t,
donc P est négligeable et
 M
M
et F  M
M  V /
V /  t
t
Bonjour excuser moi du dérangement, mais est ce que il serait possible d'aller voir mon sujet de grand oral aussi svp merci
De ce que j'ai compris parce que là il faut que je passe urgemment à la rédaction de mon grand oral , il faut que je pose mes données en les justifiant ( distance, masse,vitesse...) puis ensuite j'exprime la variation de vitesse en fonction de tout ces critère. Ensuite je justifie que la force gravitationnelle est négligeable à l'aide de la deuxième loi de Newton pour enfin trouver la fameuse intensité de force nécessaire. C'est bien ca ?
....Ensuite je justifie que la force gravitationnelle est négligeable à l'aide de la deuxième loi de Newton pour enfin trouver la fameuse intensité de force nécessaire. C'est bien ca ?
Tu écris la 2e loi de Newton durant l'impact
 M
M ( remarque: on suppose que M reste constant ici car le ou les impacteurs qui viennent s'ecraser sur A ont une masse négligeable devant M)
puis
tu justifies que la force gravitationnelle est négligeable
en calculant P tout simplement puis en comparant P à M
 V /
V /  t :
t :
P = G M MT / d2 = .....
avec MT : masse de la terre: 6. 1024 kg
M : masse de A
G = 6,7 10-11 USI (constante de la gravitation universelle)
et d = 106 km = 109 m
tu calcules ensuite M
 V /
V /  t qui vaut 1013 N en ordre de grandeur, comme on a vu.
t qui vaut 1013 N en ordre de grandeur, comme on a vu.
et tu remarques que P est négligeable devant 1013 N
Donc finalement:


 M
M  M
M  V /
V /  t
t
mais je ne pense pas que tu doives détailler tout ca.
tu fais le bilan des forces (avec un croquis!), tu dis que la 2e loi de Newton appliquée à A durant l'impact s'écrit comme indiqué plus haut, mais comme la force gravitationnelle est totalement négligeable devant F, on a le résultat : F
 M
M  V /
V /  t
t
Mais il faut que tu saches expliquer pourquoi on peut négliger P (si on te le demande)
Voila un apercu du premier truc que j'ai pu faire qu'est ec que je pourrait ajouter ?

PDF - 34 Ko
Bonjour,
Attention! pour les calculs je suis parti des données d'Apophis qui est un astéroide (géocroiseur) bcp plus gros qu'un meteore et donc vraiment dangereux et qui, d'après le web, va passer en 2029 à environ 32000 km de la terre .
taille : env. 300m
M = env. 50 .10 9 kg (donc 50 millions de tonnes)
-> ![]()
si tu prends un autre corps il faut refaire les calculs puisque la masse M change. Mais il est clair qu'on n'enverra pas des impacteurs pour un météore ni même un astéroide trop petit, vu le prix exorbitant d'une telle operation, ca ne se justifierait que pour des corps qui menacent vraiment la terre à grande échelle.
à 1 million de km de la terre, je trouve: P  107 N (en ordre de grandeur) pour Apophis
107 N (en ordre de grandeur) pour Apophis
donc on a bien P << F
Ca veut dire que la force gravitationnelle P est négligeable devant F durant l'impact,
mais avant et après l'impact, la force gravitationnelle n'est pas négligeable, elle est la seule force à agir et c'est elle qui détermine la trajectoire de A (qui est en chute libre dans le systeme solaire)
Ah c'est bon , finalement si je prend ca, et que je calculs pour mes donner de l'astéroïde ( j'ai pris les données minimum sur internet d'un astéroïde qui représenterait un danger important sans prendre un astéroïde en particulier) je trouve une force de 5,5*10^8N ( j'avoue que je préfère utiliser les newton pour donner un ordre de grandeur assez clair et en général c'est ce que les profs préfère . Est ce bon ou dois je ajouter quelque chose à mon grand oral car je finis officiellement de le taper aujourd'hui pour l'apprendre pour le 26
eBonjour, alors pour la masse j'avoue j'ai demander à chat GPT qui m'a fait un calcul avec la densité des matériaux de l'asteroide et le volume  , mais peut tu me dire si ce qu ej'ai rédiger et bien et au pire je changerais vite fait mes valeurs , juste pour la forme .
, mais peut tu me dire si ce qu ej'ai rédiger et bien et au pire je changerais vite fait mes valeurs , juste pour la forme .

PDF - 35 Ko
utiliser ChatGPT en sciences dures (physique, maths), c'est très risqué !
Même le météore que tu évoques dans ton introduction faisait déjà 12 000 t avec un diametre de 15 m ! (avec wikipédia tu aurais trouvé en 10s 
Et il est clair qu'on n' enverra jamais des impacteurs pour un "truc" aussi petit, même s'il reste malgré tout dangereux, mais pas au point d'effacer toute vie sur terre!
Voici mes commentaires puis un résumé de ce qu'on a dit dans ce fil qui pourra peut-être t'aider.
Il faudra faire revoir ca ensuite par ton prof. s'il est encore temps!
________________________
Quelle est l'intensité la force nécessaire pour dévier un astéroïde ?
15 Février 2013, un météore atterrit se désintègre au-dessus de Tcheliabinsk en Russie causant une onde de choc , des dégâts urbains énormes et des milliers de blessés . Cet incident a servi de rappel brutal de la nécessité de pouvoir dévier les astéroïdes dangereux avant qu'ils ne frappent notre planète.Mais comment éviter ce genre d'incident ? Eh bien on peut se dire tout simplement en déviant l'astéroïde en question lorsque il s'approche à une distance assez dangereuse pour la terre. Mais ce défi n'est pas si simple que ca !
Un astéroïde est un corps celeste errant dans l'espace en provenance d'une ceinture d'astéroïdes comme celle se situant entre Mars et Jupiter par ex.
(note: il y en a d'autres dans le systeme solaire qui sont plus éloignées).
Finalement, au-delà du matériel nécessaire pour pouvoir élaborer réaliser un tel projet , quelle est l'intensité de la force nécessaire pour dévier un astéroïde?
nous évaluerons un contexte bien particulier pour ensuite trouver cette intensité. Tout d'abord , il faut mettre un contexte particulier pour que chaque calcul soit à notre avantage.
Pour répondre à cette question nous allons considérer une situation simplifiée et calculer uniquement l'ordre de grandeur de la force. Le calcul précis ne peut être fait que par des agences spatiales grace à des calculs sur ordinateur.
On va observer etudier l'astéroïde par rapport à un référentiel géocentrique et lorsque nous allons effectuer cette action , l'astéroïde sera parfaitement rectiligne. Ça peut paraître insensé mais ça nous aidera dans nos calculs. On étudiera ici un astéroïde de 140 m de diamètre et de 1000 tonnes car c'est à partir de cette taille qu'un astéroïde représente un danger. Notre projet sera de devier l'astéroïde lorsque il est à une distance d'1 millions de Km( en comprenant le rayon de l'astéroïde et de la terre) pour le faire atterrir à un degré d'inclinaison très léger passer à une distance de 50000km de la terre afin de préserver les satellites en orbite. L'astéroïde avance à une vitesse constante d'environ 11km/s (ca me parait bcp, plutot 5km/s) . Pour trouver cette fameuse l'intensité de la force nous allons passer par la 2nde loi de Newton. Les forces appliquées à l'astéroïde sont la force F que nous cherchons et la force gravitationnelle. Or cette force est négligeable face au produit de la masse par l'accélération du satellite.
Mais comment a- t-on pu calculer ce résultat? Eh bien on sait que l'accélération est la dérivée de la vitesse par rapport au temps et que la dérivée et le quotient de la variation de vitesse par la variation du temps . Grâce à notre fameux petit angle d'inclinaison et nos formule trigonométrie, on se retrouve avec la variation de vitesse égale au quotient distance Terre-point d'atterrissage (b) par la distance terre-astéroïde (d) le tout multiplié par la vitesse initiale qui revient à la vitesse constant . Nous prendrons une variation du temps d'environ 1 sec car le choc est très rapide . Grâce à tout cela nous trouvons que m*a= 10^13 N . Puisque nous avons négligé la force gravitationnelle , on retrouve que la force nécessaire pour dévier l'astéroïde est égale à 10^13N.
(il faut reprendre cette partie-là ,à mon avis, regarde mon résumé plus bas, ca pourra t'aider)
Pour vous faire une petite idée , cela représente un séisme de magnitude 7,5 ou encore la force d'une bombe atomique!
(note: on peut aussi évoquer la poussée d'Ariane au décollage, de l'ordre de 5000 kN, donc 5 106N pour montrer que c'est une force énorme) Pour conclure, la force nécessaire pour dévier un astéroïde dans la situation particulière envisagée, serait de 10^13N.
Cependant, cette valeure n'est pas à prendre en considération car d'une part nous nous somme placer sur un référentiel géocentrique alors qu'un référentiel héliocentrique serait plus adéquat , nous avons mis l'astéroïde à une trajectoire parfaitement rectiligne et le traitement du choc mou pour l'astéroïde aurait été plus approprié que la seconde loi de Newton mais cela dépasse notre programme de Terminale
Cette valeur n'est qu'un ordre de grandeur car nous avons fait beaucoup d'approximations.
_________________________________________________________
Résumé de notre discussion:
Quelle est la force nécessaire pour dévier un astéroide ?
Pour répondre à cette question nous allons considérer une situation simplifiée et calculer uniquement l'ordre de grandeur de la force. Le calcul précis ne peut être fait que par des agences spatiales grace à des calculs sur ordinateur.
Nous nous placons dans le referentiel géocentrique.
Supposons qu'un astéroide A, situé à une distance d = .... km de la terre T, se dirige droit sur elle à une vitesse de plusieurs km/s.
L'idée est de modifier la vitesse de A pour qu'il se ne dirige plus droit sur la terre, mais vers un point H situé à une certaine distance b du centre de la terre, comme on peut le voir sur ce schéma. (-> à ce stade je pense qu'il faut montrer un schéma assez grand et clair, comme celui que j'avais fait le 17.6 à 20:55 pour expliquer au jury)
Un rapide calcul montre que la variation de vitesse à communiquer à A vaut alors: (en supposant b << d donc l'angle alpha petit)
ΔV = b Vo / d
En fait l'asteroide ne passe pas en H mais va passer plus près de la terre car il est dévié par la force de gravitation de la terre, comme le montre la trajectoire en pointillés sur le schéma. Mais nous nous contenterons de la formule approchée et nous prendrons une valeur de b suffisamment grande pour avoir une marge de sécurité.
La deuxieme étape du calcul consiste à évaluer la force nécessaire pour modifier la vitesse de A de ΔV.
Cette force est fournie par un (ou plusieurs impacteurs), c'est-à-dire des sondes lancées vers A depuis la terre, et qui viennent s'écraser sur A avec une très grande vitesse (plusieurs km/s).
Lors de l'impact, A est soumis à 2 forces:
La force F due à 1 ( ou plusieurs) impacteurs
et la force gravitationnelle P de la terre
Or P est ici négligeable devant la force de l'impact (ce qu'on peut vérifier par le calcul en calculant P et en comparant à F),
donc les lois de la mécaniques (2e loi de Newton) permettent d'écrire:
F  M ΔV / Δt
M ΔV / Δt
où M est la masse de A
et Δt la durée du choc (très bref et très violent!)
En combinant les deux égalités trouvées, nous pouvons donc écrire que la force nécessaire vaut environ :
F = M b Vo / (d Δt)
Application numérique:
Pour un astéroide de 150 m environ (considéré comme dangereux), on peut prendre:
M = 5 millions de tonnes (5. 109 kg)
Vo = 5 km/s (par rapport à la terre)
d = ... millions de km
Δt = 1s
Pour le calcul de b il faut savoir que le rayon terrestre est de 6400 km. Si on ajoute l'atmosphère on arrive à 6600 km. D'autre part si on veut éviter des collisions avec les satellites les plus hauts en orbite autour de la terre (les satellites géostationnaires utilisées pour les communications) , il est préférable d'ajouter encore 36000 km. Donc on peut prendre b = 50000 km par ex. (le calcul précis de b ne peut être fait que par les agences spatiales).
Avec ces données, on trouve une force F = .... N
Ma conclusion n'est pas bonne ? Pourtant c'est ce que je préférait et ça montrait que le programme de terminale était limiter 😊. Et le problème est que je ne peut pas montrer de schéma au jury , on ne peut pas utiliser le tableau . Et j'ai mis un peu de bla-bla pour essayer de bien durer 5 min lors de la presentation
Tu peux montrer un schema sur une feuille A4 que tu prepares a l avance durant les 20 min avant de passer devant le jury, tu peux meme en faire plusieurs, car je ne vois pas comment parler de physique sans dessin!!!
Tu peux meme en faire un autre avec les formules et les valeurs numeriques pour la discussion. En fait tu prepares ce que tu veux, mais effectivement tu ne peux pas utiliser le tableau.
Pour ta conclusion, elle est trop negative, a mon avis, on a l'impression que ton calcul est totalement faux or ce nest pas vrai. Il nest pas precis, cest vrai, mais l'ordre de grandeur est bon à mon avis. Le probleme c'est d'evaluer b et d en fait .
C'est pour ca que j'ai resumé.
Si tu veux insister sur les approximations faites et la facon de faire le calcul precis, tu peux ajouter:
Pour le vrai calcul, il faudrait se placer dans le referentiel heliocentrique pour tenir compte de linfluence du soleil, puis faire le calcul de la trajectoire precise de A qui est devié par la terre, et eventuellement la lune, pour mieux evaluer b , et enfin utiliser les lois du choc pour obtenir F. Mais tout ceci est hors de portee d'un eleve de Terminale .
Lorsque A est a plusieurs millions de km de la terre, la force gravitationnelle du soleil est dominante (sauf evidemment si A se rapproche bcp d'une autre planete comme jupiter par ex.)
La sphere d'influence de la terre a un rayon d'un million de km env. je crois.
Ca depend de la masse de l'astre.
Je ne sais pas si vous êtes toujours là , je passe dans moins de 2h et je voudrais savoir comment justifier la distance d
pour un asteroide provenant de la ceinture entre Mars et Jupiter, la distance d peut dépasser les 100 millions de km, mais au delà de qqes millions de km, on ne peut plus utiliser le ref. geocentrique car l'influence du soleil devient alors prédominante et les calculs de trajectoire se compliquent nettement...
Bon bah finalement je viens de passer sur l'autre sujet …
En tout cas merci du fond du cœur pour toute l'implication que vous avez eu et l'aide que vous m'avez fournie j'en suis reconnaissante et j'ai appris plein de chose .
Bonne continuation


