Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

frottements quadratiques

Posté par
nimeile 12-03-24 à 14:15

bonjour a tous
je sollicite votre aide car j'ai du mal a comprendre un exercice

voici l'énoncer:

Les orages en montagne sont courants , et il arrive régulièrement qu'ils soient accompagnés de chutes de grêle.
La grêle est constituée de blocs de glace , appelés grêlons ,de formes variées et de tailles pouvant aller de quelques millimètres à plusieurs centimètres.
Ces blocs se forment au sein des nuages ,à des altitudes comprises entre 1 et 10km. Leur vitesse de chute au sol avoisine les 100km⋅h−1 pour des grêlons de 4 à 8 centimètres de diamètre . Cette partie s'intéresse à la modélisation de leur chute.

les question de la partie 1.1 et 1.2 sont sur l'image

j'ai pu répondre a la première partie sans problème

mais concernant la seconde partie je n'arrive pas comprendre comment obtenir l'équation différentiel avec ces information je ne fait pas non plus le lien avec ce que me dit mon cour où F =−βv v(vecteur)

je sollicite donc votre aide afin de m'éclairé sur la démarche  a suivre

cordialement
merci beaucoup

(image tiré d'un exercice de B.pagani)




frottements quadratiques

Posté par
vanoisere : frottements quadratiques 12-03-24 à 14:52

Bonjour
Si je comprends bien, tu est rendu à la question 4 partie 1.2 ;
Quelles sont les forces exercées sur le grêlon ? Appliquer alors le principe fondamental de la dynamique.
Question 5 : réfléchir à ce qui se passe au cours de la chute quand la vitesse augmente.

Posté par
vanoisere : frottements quadratiques 12-03-24 à 16:48

Pour t'aider un peu, voici une simulation de la courbe v=f(t) et de la courbe z=g(t)...

frottements quadratiques

frottements quadratiques

Posté par
nimeilere : frottements quadratiques 13-03-24 à 12:49

bonjour
je vous remercie pour les simulation, cela m'aide grandement !

pour le PFD j'ai :

\sum \vec{F}ext=m.\vec{a}

en suivant cette expression, dans mon cas les forces appliqué a mon système sont:

-la pesanteur
-les force de frottement

donc \sum \vec{F}ext= \vec{f} + \vec{P}

j'ai un doute sur  sur le fait que la masse la masse fait partie de force extérieur

Posté par
vanoisere : frottements quadratiques 13-03-24 à 13:52

Citation :
j'ai un doute sur  sur le fait que la masse la masse fait partie de force extérieur

Confusion de ta part entre masse et poids ?
Le poids est une force attractive exercée sur le grêlon par la terre. C'est donc bien une force exercée sur le grêlon par le milieu extérieur.
Pour ne pas avoir de problème, je te conseille de toujours définir une force par :
action exercée sur ... par ...  (pointillés à remplacer)
Une force extérieure correspond à "action exercée sur le système par le milieu extérieur".
Reste maintenant à projeter la relation vectorielle  que tu as obtenue,correspondant à la relation fondamentale de la dynamique, sur l'axe (Oz) défini par l'énoncé. Cela te donnera l'équation différentielle vérifiée par la vitesse.

Posté par
nimeilere : frottements quadratiques 14-03-24 à 06:45

donc j'ai \sum \vec{F}ext = -\alphav2\vec{e}z+m\vec{g} = m\vec{a}

\Rightarrow  m\vec{a} +\alphav2\vec{e}z = m \vec{g}

\Rightarrow  m\frac{d v}{dt}+\alpha \vec{v}v=m \vec{g}

\Rightarrow \frac{d v}{dt} + \frac{\alpha \vec{v}}{m}v=\vec{g} \\



j'ai du mal avec les projection mais en essayant j'obtient:

\Rightarrow \left\lbrace\begin{matrix}\frac{d v(x)}{dt} + \frac{\alpha \vec{v}}{m}v=0 \\ \frac{d v(y)}{dt} + \frac{\alpha \vec{v}}{m}v=0 \\ \frac{d v(z)}{dt} + \frac{\alpha \vec{v}}{m}v=\vec{g} \end{matrix}\right.

Posté par
vanoisere : frottements quadratiques 14-03-24 à 10:15

Tu te compliques la vie. L'énoncé précise qu'il s'agit d'une chute verticale descendante. Il suffit de projeter sur un axe (O,z) vertical orienté vers le bas.

Posté par
nimeilere : frottements quadratiques 14-03-24 à 11:37

en faisant plus simplement j'obtient:

\ddot{z} + \frac{\alpha }{m}\dot{z}2=\vec{g}

je ne vois pas comment faire autrement !

Posté par
vanoisere : frottements quadratiques 14-03-24 à 12:07

Tu y es presque. Tu as simplement oublié de projeter aussi le vecteur \vec g
Dans la mesure où l'énoncé demande l'équation différentielle vérifiée  par v(t) et non celle vérifiée par z(t), j'écrirais plutôt :

\dfrac{dv_{(t)}}{dt}=-\dfrac{\alpha}{m}\cdot v_{(t)}^{2}+g
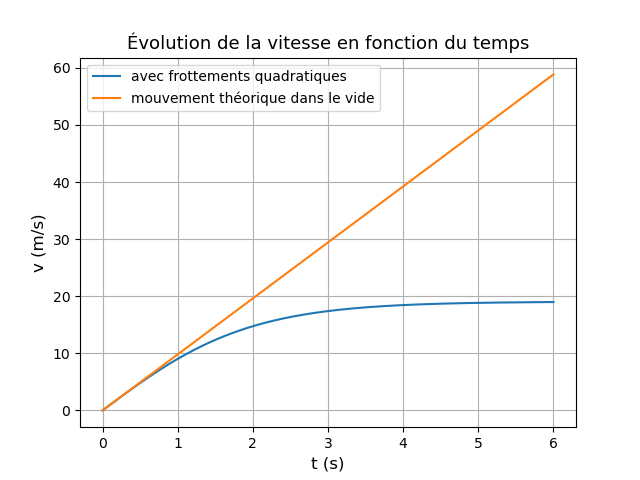
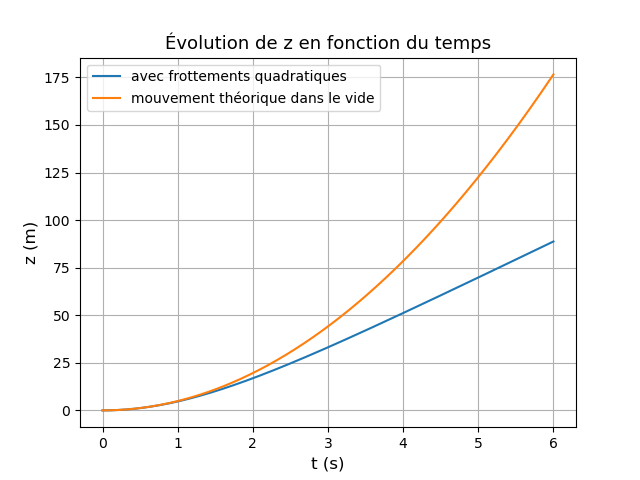
En laissant l'équation différentielle sous cette forme, il me semble plus facile de répondre à la question 5. Tu peux aussi t'aider des courbes que je t'ai fournies.

Posté par
nimeilere : frottements quadratiques 14-03-24 à 12:29

je vous remercie grandement

pour la question 5, j'ai supposé que pour avoir une vitesse limite il faut que l'accélération soit nul donc:

\frac{dv}{dt}=0

comme g est une constante alors -\frac{\alpha }{m}v _{(t)}^2  doit être égale a -g


pour l'expression je propose \sqrt{\frac{g}{a}m}=v_{lim}


Posté par
vanoisere : frottements quadratiques 14-03-24 à 13:38

C'est bien cela. L'équation différentielle montre que, plus la vitesse augmente plus l'accélération diminue et donc, comme tu l'as écrit, l'accélération finit par devenir nulle.

Posté par
nimeilere : frottements quadratiques 14-03-24 à 13:42

D'accord, je vous remercie pour votre aide, astuce et graphique cela m'a grandement aider.  


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !