Inscription / Connexion Nouveau Sujet
Force sur un plan incliné avec frottement
Bonjour, je dois trouver la force en newton qu'il faut pour pouvoir amener une pierre en la tirant à l'aide de cordes jusqu'en haut d'une rampe en brique crue, la pierre repose sur un traineau en bois, admettons que le traineau ne pèse rien, la pierre pèse 2.5 tonnes et l'angle de l'inclinaison de la rampe est de 20°, je sais qu'il faut prendre en compte le frottement etc... j'ai essayé de comprendre comment faire a l'aide de vidéos mais je n'y arrive toujours pas et je dois bientôt terminer cela alors si quelqu'un pouvait m'aider ça serait vraiment gentil, merci 
Ah la mécanique...elle nous perd tous!
Commence par faire le bilan des forces: ici le poids, la réaction du support et les frottements. Avec un schéma ce sera plus facile et il est demandé au bac pour justifier ton choix d'axes 
Après il faut que tu projettes selon tes axes (Ox) et (Oy), je pense que tu as déjà fait ça en cours, sinon je t'expliquerais comment faire
Le frottement a un coefficiant de 0,6 et le poids de 2.5kg, les axes oui je les ai placés sur un schéma donc ça, ça va 
mais je connais pas les formules a part les bases mais je ne sais pas comment trouver la force quand même 
Voila déjà le poids (qui en fait est une masse) qui est redescendu de 2,5 tonnes à 2,5 kg entre ton 1er et to, 2ème message.
"les axes oui je les ai placés sur un schéma donc ça"
Oui, mais encore ?
Il y a une infinité de manière de placer les axes, plein de "pas bonnes" et quelques unes de judicieuses.
Commence par citer toutes les forces agissant sur la pierre et précise , leurs directions et leur sens ...
Le mieux est de faire un dessin en représentant toutes ces forces (pas besoin d'être à l'échelle) et de dessiner les axes que tu as choisi ... et d'envoyer ce dessin sur le site
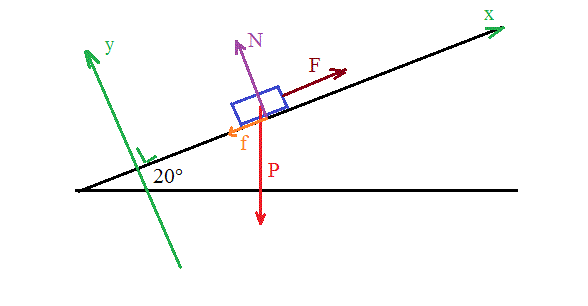
Bilan des forces sur la pierre :
a) son Poids : P = mg (vertical, vers le bas)
b) Composante de la réaction du support normale au support : N (vers le haut)
c) Composante de la réaction du support tangentielle au support : f (vsens opposé au mauvement)
d) Force exercée sur la corde (supposée // à la ligne de plus grande pente du plan incliné, vers le haut)
Projection des forces sur l'axe des y :
N - P.cos(20°) = 0
N = 2500 * 9,81 * cos(20°) = 23046 N
---
Projection des forces sur l'axe des yx
F - f - P.sin(20°) = R (avec R la résultante des forces sur la Pierre (vers le haur du plan incliné)
On doit avoir R >= 0 et donc F min = f + P.sin(20°)
Or f = 0,6.N = 0,6 * 23046 = 13828 N
F min = 13828 + 2500*9,81*sin(20°) = 22216 N
Arrondir pour nombre de chiffres significatifs si c'est attendu.
Sauf distraction. (calculs non vérifiés).
Annuler
connectez vous