Inscription / Connexion Nouveau Sujet
Force de traction - Force de réaction au sol
Bonsoir,
Je bloque sur une question pour un devoir maison sur le travail des forces.
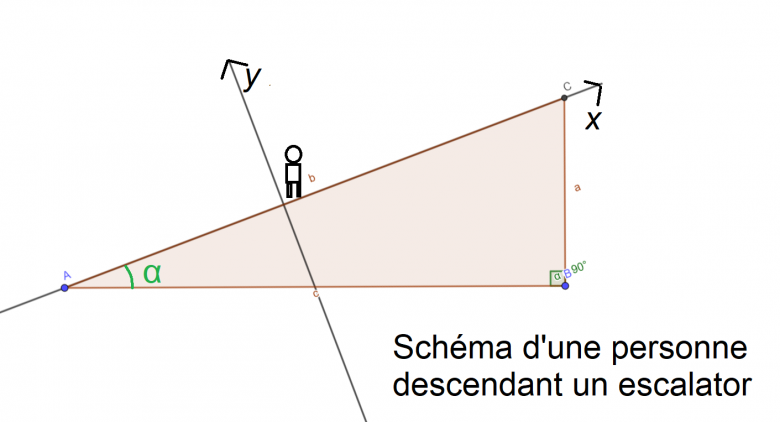
Nous avons une personne de 75 Kg sur un escalator de 50 m de long, AC sur le schéma, avec un angle α de 30° par rapport au sol (Schéma ci contre). On nous précise que la personne sur l'escalator est mouvement rectiligne et a une vitesse constante.
On a du projeter le vecteur du poids de la personne en fonction des axes x et y et ses coordonnées. (J'ai trouvé x=-cosα et y=-sinα)
Et en deuxième question on doit "en déduire la valeur de la force de traction des escalators et de la réaction au sol" Et je bloque ici.
C'est ici que je vous appelle à l'aide. Pourriez vous me débloquer de cette impasse s'il vous plait ?
Bonjour,
Il te faut tout d'abord revoir tes projections du poids.
Celles que tu as trouvées seraient les mêmes pour un enfant de deux ans, pour l'homme de l'énoncé (75 kg) ou bien pour un colosse genre Teddy Riner.
Ca ne va pas.
Ensuite je te suggère de faire l'inventaire des autres forces qui s'exercent sur cette personne et d'appliquer le principe d'inertie ( ou première loi de Newton )
Alors, il est vrai que j'hésitais avec cette projection de poids (x= -P(init)xcosα) et (y= -P(init)xsinα) avec P=mg.
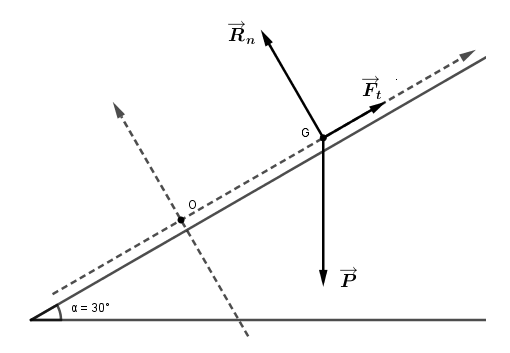
Oui donc on aurait P + Rn + Ft = 0 (P: Poids; Rn: Reaction au sol; Ft: Force de traction)
Je néglige les frottements.
Mais j'ai deux inconnus Ft et Rn.
La relation correcte est une relation vectorielle :
En la projetant sur l'axe Ox, tu obtiendras de quoi répondre à la question sur la force de traction.
En la projetant sur l'axe Oy, tu obtiendras de quoi répondre à la question sur la réaction.
D'accord donc j'ai fait mon etude en séparant le cas Oy et Ox:
(Je n'arrive pas à mettre les flèches pour les vecteurs donc on va dire qu'elles sont là)
Ox:
Rn est nul
P (Vecteur) = -P.sin a = -(mg) sin a = -(75*9.81)*0.5=-367 N
Donc Ft = 367 N
Oy:
Ft est nul
P (Vecteur) = -P.cos a = -(mg) sin a = -636N
Donc Rn =636N
Par contre je comprend pas que la traction soit positive étant donné que la personne descende ?
Est ce que je me suis trompé dans mon raisonnement ?
On part de la relation vectorielle :
La projection de cette relation sur Ox est :
- P * sin( ) + 0 + Ft = 0
) + 0 + Ft = 0
ce qui donne Ft = P * sin( ) = 75 * 9,8 * 0,5 = 367,5N
) = 75 * 9,8 * 0,5 = 367,5N
Et la projection sur Oy est :
- P * cos( ) + Rn + 0 = 0
) + Rn + 0 = 0
Rn = P * cos( ) = 75 * 9.8 * 0,866 = 636,5 N
) = 75 * 9.8 * 0,866 = 636,5 N
Les intensités des forces sont toujours positives quelles que soient leurs directions et leurs sens.
Remarque : Je ne sais pas pourquoi tu dis que la personne descend.
Ah oui, je viens de voir pourquoi tu dis qu'elle descend !
Cela ne change en rien la solution.
La force de traction s'exerce tout de même vers le haut de l'escalator et puisque le mouvement est rectiligne et uniforme on a toujours conformément à la première loi de Newton :


