Inscription / Connexion Nouveau Sujet
Force centripète dans théorème énergie cinétique?
Bonjour.
Voici mon ennonce:
On schématise ci dessous le trajet d'une luge, supposée ponctuelle et de masse m=1kg lâchée sans vitesse initiale à partir du point haut A et descendant le long d'un parcours AM.
La dénivellation h est de 500 m. On négligera les frottements.
Je ne peux pas vous faire de schéma avec mon téléphone malheureusement.
Imaginer que le parcours représente une droite incliné vers le bas, et la fin de la trajectoire se termine par un arc de cercle
. J'espère que c'est assez parlant pour vous 
On nous a demandé de calculer la vitesse en b (facile)
Puis d'exprimer les différentes forces en fonction de la loi fondamentale de la dynamique (pas de problèmes rencontres)
Et la viens ma question, on me demande d'exprimer le théorème d'énergie cinétique:
Donc moi je trouve:
1/2mVM² - 1/2mVb² = -mgr(1-cosTHETA)
La correction m'indique:
(mV² /r)-(mVB²/r)=-mgr(1-cosTHETA)
Je me demande si ils n'ont pas incorporé la formule de la force centripète ?
bonjour,
Précise la trajectoire. où est B? où est M?
(mV² /r)-(mVB²/r)=-mgr(1-cosTHETA)
Cette égalité est manifestement fausse:
à gauche: des forces: mV²/r ...
à droite: un travail: mgh
(je suppose que r est le rayon du cercle)
ok car mon livre me dis que le théorème de l'énergie cinétique permet d'écrire (mV² /r)-(mVB²/r)=-mgr(1-cosTHETA)
je te donne ce schéma pour y voir plus claire
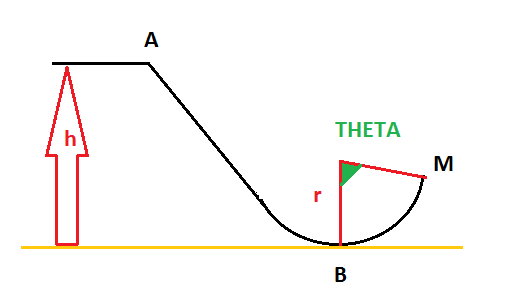
La bonne réponse est : 1/2 m.VM² + m.g.r(1-cos(theta)) = 1/2 m.Vb²
Pourquoi on ferait intervenir une force d'inertie alors qu'on se place dans un référentiel tout à fait galiléen ?! Et puis la force centripète serait normale au vecteur vitesse n'est-ce pas ?
je ne comprends pas les "/r" que tu sembles voir dans le corrigé, en effet ça ne serait pas homogène


