Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Reprise d'études [tout]Lister tous les topics de physique - chimie
Niveau reprise d'études
Partager :

Filtre Rc. Diagramme de bode

Posté par
Krampish 31-01-23 à 09:50

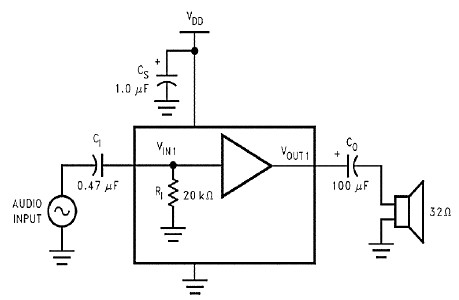
Soit le circuit en PJ.



1.quelle est la nature du filtre et la fréquence de coupure du filtre formé par C1 et R1 ?

Tracer l'allure du diagramme de bode



2. quelle est la nature du filtre et la fréquence de coupure formé par C0 et RH = 32 ohms du casque audio sur la sortie de l'amplification ?



Pour tracer le point 1, j'essaie de trouver la fonction de transfert :



F(T)= Vs / Ve = RjCw/1+RjCw


A partir de là, je n'arrive pas à appliquer ce que j'ai appliqué pour tracer le diagramme de bode.



              |                                           106

RjCw     |                1                       |         1

1/ RjCw |                0                    |         -1

G           |                 1                      |          0


Je crois qu'il y a une énorme erreur….

Sûrement au niveau des points de cassures….

Je trouve comme point de coupure pour :

RjCw vaut 9.4.10^-3

Détermination du 1er point :

20 log (K) -m.a.20

m = indice de 10^x sur le diagramme de bode.

Je pose m = 1

K= 1

a = 1 ; Fonction de transfert de rang 1

soit 20log1 - 1.20 = -20 dB

En vous remerciant

Filtre Rc. Diagramme de bode

Posté par
Krampishre : Filtre Rc. Diagramme de bode 31-01-23 à 09:53

Voici le diagramme de bode pour le point 1.

Cordialement

Filtre Rc. Diagramme de bode

Posté par
vanoisere : Filtre Rc. Diagramme de bode 31-01-23 à 11:06

Bonjour
Le filtre R1C1 est un passe-haut du premier ordre. Pour son diagramme asymptotique, tu peux étudier les deux cas limites :
R1C1<<1 et R1C1>>1.
La fréquence de coupure correspond au cas particulier d'un module H de la fonction de transfert égal à Hmax/2.

Posté par
Krampishre : Filtre Rc. Diagramme de bode 31-01-23 à 11:14

Bonjour Vanoise.

Je suis confronté à un problème, que tu avais compris la détermination de la fréquence de coupure.

Je suis incapable de dire ce que j'ai trouvé est juste.

J'ai vu une formule.

Fc= 1/2pi.r.c

Mais quand je calcule moi je ne trouve pas le même résultat.

La particularité dont tu parles c'est pour tous passe haut

Posté par
vanoisere : Filtre Rc. Diagramme de bode 31-01-23 à 11:36

\underline{H}=\frac{jR_{1}C_{1}\omega}{1+jR_{1}C_{1}\omega}\quad;\quad H=\frac{R_{1}C_{1}\omega}{\sqrt{1+\left(R_{1}C_{1}\omega\right)^{2}}}

H_{max}=1 (valeur asymptotique obtenue quand la fréquence tend vers l'infini)

La pulsation de coupure correspond à :

H=\frac{H_{max}}{\sqrt{2}}=\frac{1}{\sqrt{2}}

2H^{2}=1\quad;\quad2\left(R_{1}C_{1}\omega_{o}\right)^{2}=1+\left(R_{1}C_{1}\omega_{o}\right)^{2} \\

R_{1}C_{1}\omega_{o}=1

Cela conduit bien à la formule que tu fournie pour la fréquence de coupure.

Posté par
Krampishre : Filtre Rc. Diagramme de bode 31-01-23 à 11:43

Merci Vanoise.

Je ne sais pas après tes réponses' si j'ai juste ou faux.

Désolé.

Posté par
vanoisere : Filtre Rc. Diagramme de bode 31-01-23 à 13:58

L'allure de ton diagramme de Bode du gain est correcte mais attention aux graduations des axes. Les exigences ne sont pas exactement les mêmes d'une filière à l'autre mais dans tous les cas, il est intéressant de remarquer :

R_1C_1\omega=\frac{\omega}{\omega_{o}}=\frac{f}{f_{o}}

ce qui permet d'écrire la fonction de transfert sous la forme :

\underline{H}=\frac{j\frac{f}{f_{o}}}{1+j\frac{f}{f_{o}}}


Tu peux graduer l'axe des abscisses en décades : \frac{f_{o}}{100},\frac{f_{o}}{10},f_{o},10f_{o},100f_{o}...
L'application numérique conduit à fo=17Hz ce qui est cohérent avec le fait que l'oreille capte les sons de fréquences supérieures à 20Hz environ. Le filtre laisse passer les signaux audibles et atténue les parasites de très basses fréquences.

Attention : un diagramme de Bode est constitué de deux courbes : celle du gain à laquelle tu penses et celle de la phase que tu as tendance à oublier...

Posté par
Krampishre : Filtre Rc. Diagramme de bode 31-01-23 à 15:03

Bonsoir,

Oui effectivement je zappe souvent le graphe des phases.

Mais le plus dur c'est le diagramme du gain. Qui me fait mal à la tête. Franchement.

Tu trouves 17 Hz.

Mais avec ton aide je n'arrive pas à arriver à ce résultat.

Hormis quand j'utilise bêtement la formule.

Fc= 1/(2.pi.r.c)

Je ne connais pas f et ni w, ni w0.
Je peux calculer w0= 1/R1.C1= 106 rad/s

Posté par
vanoisere : Filtre Rc. Diagramme de bode 31-01-23 à 15:14

Citation :
Je peux calculer w0= 1/R1.C1= 106 rad/s

D'où la fréquence de coupure :
fo=o/(2)17Hz

Posté par
Krampishre : Filtre Rc. Diagramme de bode 31-01-23 à 15:23

Citation :
ce qui est cohérent avec le fait que l'oreille capte les sons de fréquences supérieures à 20Hz environ. Le filtre laisse passer les signaux audibles et atténue les parasites de très basses fréquences.



Est ce une information qui doit être connue par tout le monde ou c'est à apprendre dans le cours ?

Posté par
vanoisere : Filtre Rc. Diagramme de bode 31-01-23 à 15:50

Cela fait partie de la culture scientifique ...
Les fréquences audibles sont comprises entre environ 20Hz pour les graves et environ 20kHz pour les graves. Bien sûr, ces fréquences limites varient un peu d'une personne à l'autre et varient en fonction de l'âge.

Posté par
Krampishre : Filtre Rc. Diagramme de bode 31-01-23 à 16:12

Bonsoir,

Je me rends compte que la méthode que j'ai vu pour déterminer le premier point est nulle.

20log K- m.a.20

Je ne trouve rien de cohérent.

Si je veux tracer un diagramme avec les fréquences en abscisse et gain en ordonnées.

Je dois trouver la valeur du module quand f tend vers 0

Soit rac(f/f0) ^2  = 20 logf- 20 log 17= 20log0 - 20 log 17 = 24.60 dB
Et
Soit  rac(1+f/f0) ^2 tend vers 1

On obtient-20log17-20log1 = - 24.60dB

Quand f tend vers infini.
rac( f/f0) ^2 tend vers f/f0
Et
Soit  rac(1+R. C. f/f0) ^2 tend vers f/f0 également.

Donc 20 log (f/f0 /f/f0) = 20 log 1= 0
Donc cela tend vers 0 quand f tend vers +infini.

Posté par
vanoisere : Filtre Rc. Diagramme de bode 31-01-23 à 16:31

Pour le même prix, je mème de front les deux diagrammes asymptotiques.

1° cas : basses fréquences telles que f<<fo donc telles que f/fo<<1 :

\underline{H}\approx j\frac{f}{f_{o}} donc : \varphi\approx\frac{\pi}{2} et G\approx20\log\left(\frac{f}{f_{o}}\right) : asymptote oblique de pente +20dB/décade

2° cas : hautes fréquences telles que f>>fo donc telles que f/fo>>1 :

\underline{H}\approx1 donc : \varphi\approx0 et G\approx0

Voici le tracé réel du diagramme avec fo=17Hz.

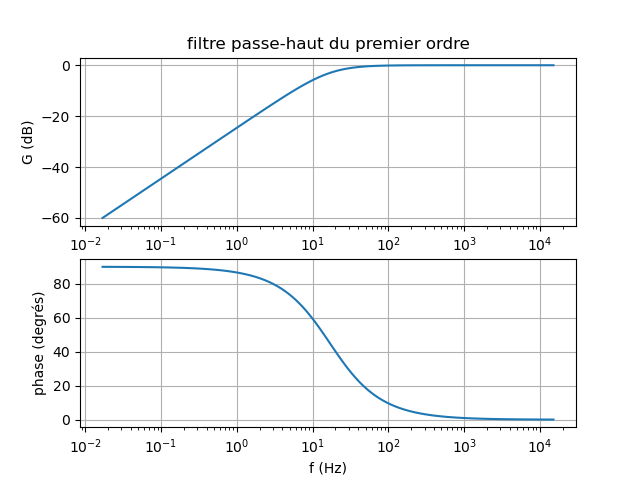
Filtre Rc. Diagramme de bode

Posté par
Krampishre : Filtre Rc. Diagramme de bode 31-01-23 à 16:51

Je ne comprends pas comment tu arrives à-60dB.

J'ai fait quand f tend vers 0 c'est Le même raisonnement. Non ?

20log(f/f0) - 20 log (1+ f/f0)
20 log f - 20 log f0 - (20 log 1 +(20log f- 20 logf0)
0 - 20 log17 - (0 + (0- 20log17)
-20log 17 +20 log17

Échec.....

Posté par
Krampishre : Filtre Rc. Diagramme de bode 31-01-23 à 16:59

Je pense que j'ai compris.
Tu prends une fréquence au hazard et tu remplacés f par la valeur prise.

Par exemple.

Si f = 10^-2 je trouve-64dB

Posté par
vanoisere : Filtre Rc. Diagramme de bode 31-01-23 à 19:09

OK. Petit complément : si tu veux tracer l'allure du diagramme réel ayant le diagramme asymptotique, tu peux placer les points correspondant à f=fo. A cette fréquence propre :
G=Gmax-3=-3dB
=/4 rad (45°)
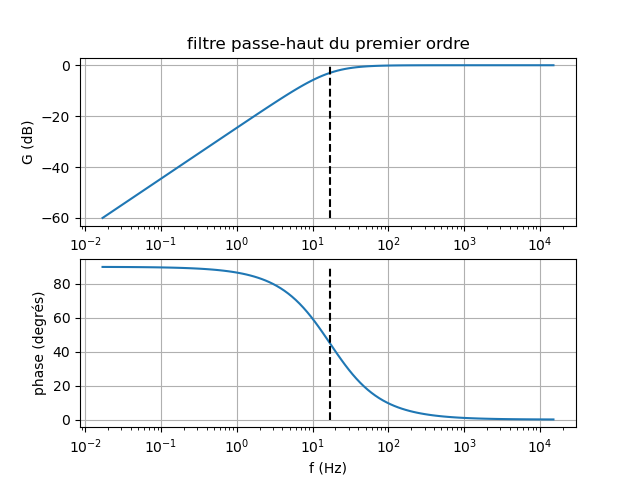
Pour visualiser cela, j'ai ajouté les verticale en pointillés d'abscisse f=fo=17Hz.
Il suffit alors de terminer le tracé à "main levée".

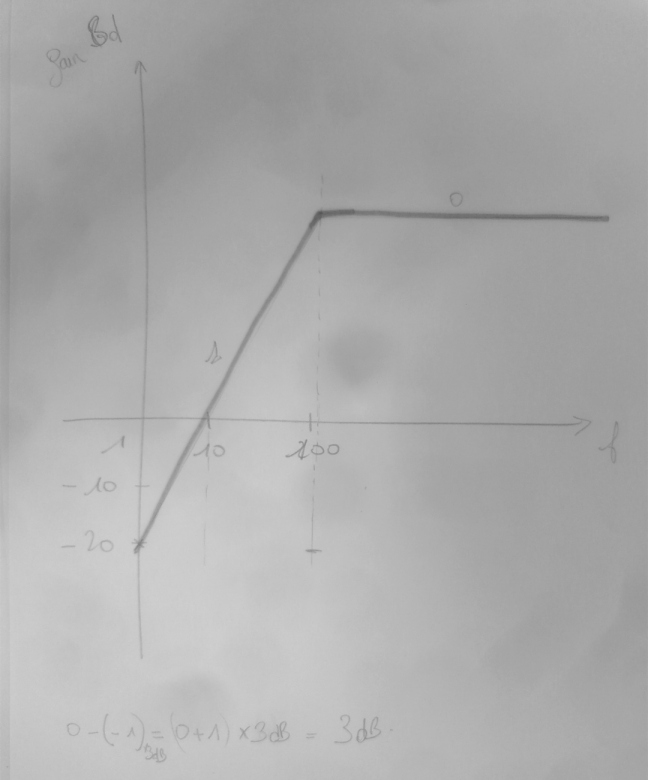
Filtre Rc. Diagramme de bode


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !