Bonjour,

Je bloque sur un exercice de Physique.
Voici l'énoncé ainsi que mes réponses.


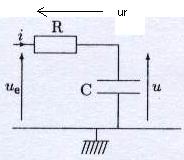
Soit une tension sinusoïdale imposée par un générateur. Le but de ce problème est d'étudier ce filtre, c'est-à-dire de savoir ce que vaudra en fonction de la fréquence de la tension d'entrée u. La tension d'entrée est sinusoïdale, c'est-à-dire que , où est la pulsation de la tension (reliée à sa fréquence par ) et est son amplitude.

1. Établir l'équation différentielle vérifiée par . On posera .

2. On peut montrer qu'en régime forcé comme on est ici, la tension est une fonction sinusoïdale de pulsation . On peut donc chercher la solution sous la forme , où est l'amplitude, inconnue, de la tension , et est son déphasage par rapport à la tension . Réinjecter la forme de solution propose dans l'équation différentielle, puis dévelepper les cosinus et sinus à l'aide des formules de trigonométrie.

3. Identifier les termes en et de part et d'autre du signe égal. On a à présent deux équations à deux inconnues : et (qui apparaît sous forme de et .

4. Exprimer en en fonction du reste des variables.

5. En déduire l'expression de en fonction de et .

6. En écrivant que , en déduire l'expression de en fonction de et .

7. On posera et . Donner l'expression de et en fonction de .
______________________

1. loi des mailles :
   loi d'ohm :
   relation caractéristique du condensateur :

d'où ou encore .

2. Après réinjection de la solution proposée dans l'équation différentielle, on aboutit à .

Après développement, .

3. "Identifier les termes en et de part et d'autre du signe égal" c'est-à-dire ? Je ne comprends pas ce qu'il faut faire...

4. Je trouve cos(\phi)[Usin(\omega t)-\omega_0Ucos(\omega t)]+sin(\phi)[Ucos(\omega t)+\omega_0Usin(\omega t)]+u_e\omega_0=0.

D'où cos(\phi)=\frac{-sin(\phi)[Ucos(\omega t)+\omega_0Usin(\omega t)]-u_e\omega_0}{Usin(\omega t)-\omega_0Ucos(\omega t)} et sin(\phi)=\frac{-cos(\phi)[Usin(\omega t)-\omega_0Ucos(\omega t)]-u_e\omega_0}{Ucos(\omega t)+\omega_0Usin(\omega t)}.

Je trouve ça bizarre du coup je bloque...

Merci d'avance et passez tous de bonnes fêtes de fin d'année !