Inscription / Connexion Nouveau Sujet
Filtrage/Diagramme de Bode
Bonjour,
J'ai eu mon bac STI Electronique il y a 20 ans. Pour mon travail je dois faire une préparation niveau bac+2 qui me plonge dans les maths et la physique.
J'avais déjà posté sur un autre sujet et j'avais apprécié les pistes données pour avancer dans un devoir.
Cette fois-ci il s'agite de devoirs sur les filtrages et les diagrammes de Bode (c'est peut-être un sujet que j'aurais dû mettre dans le forum de lycée).
Exerice n°1
On considère un filtre de fonction de transfert
H(j
=20/((1+0.2j)(1+10j))
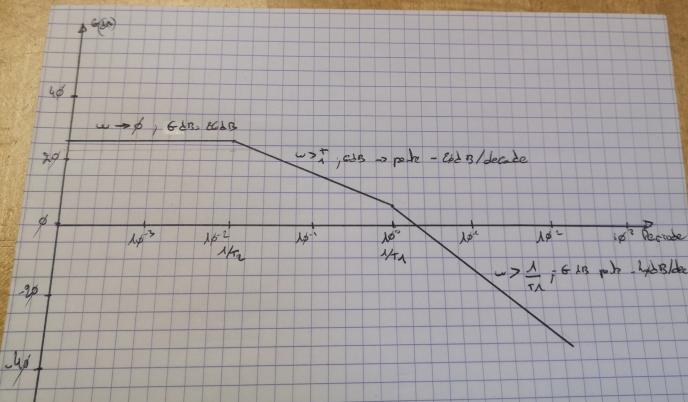
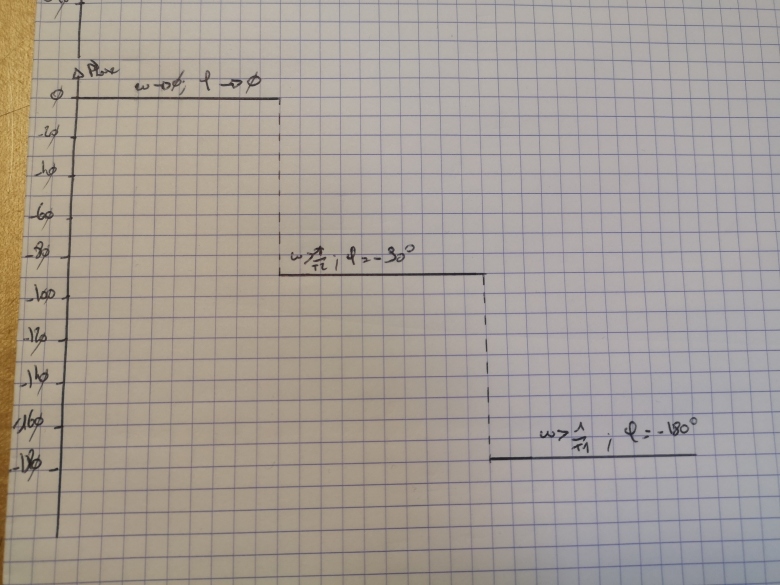
a/ Tracer le diagramme de Bode asymptotique de cette fonction
Je suis parti sur la décomposition de la fonction en sous-élément
H0=20
H1=1/(1+0.2j)
H2=1/(1+10j)
Pour H0
|H0|=20
G|H0|=20Log(20)=26dB
ArgHo=0
Pour H1
|H1|=1/
(1+(0.2)²)
G|H1|=20Log1-20Log(1+(0.2)²)
G|H1|=-20Log(1+(0.2)²)
0
G|H1|=0dB
ArgH1=0
+
G|H1|=-20Log(] soit une pente de -20dB/décade
ArgH1=-
/2
Pour H2
0
G|H2|=0
ArgH2=0
+
G|H2|=-20Log(] soit une pente de -20dB/décade
ArgH2=-/2
Pour mon tracé
1/T2=1/10<1/T1=1/0.2
b/ Préciser les pulsation de cassure
On sait que les fréquences de coupures = Gmax-3dB
c1
Gmax-3dB=26-3=23db
c2
23dB-20dB=3db
Gmax-3dB=3-3=0dB
(ils ne sont pas mis sur mon diagramme car j'avais pris la photo avant de les positionnés)
Comme je bosse tout seul le soir après le travail j'aimerais savoir si ces réponses vous semble correcte (au moins savoir si j'ai compris cette partie ou non).
Merci d'avance pour vos réponses
Bonjour,
Le diagramme est tracée en pulsation ?
Il doit être tracé de manière exacte numériquement ou juste en principe ?
Si c'est en principe c'est correct, sinon en pulsation, comme vous l'avez vous-même indiqué, les cassures doivent se produire pour 0,1 et 5.
Je n'ai pas compris votre calcul pour le G de la deuxième cassure : je trouve -11 dB.
Il n'y a rien de précisé dans l'énoncé.
Du coup je suis partie sur un tracé sur la période.
Aurais peut-être du prendre la pulsation ?
Il n'y a rien non plus de précisé sur le tracé "numérique" ou juste de "principe"
Du coup je suis parti sur du principe.
Juste pour savoir si je devais faire un tracé numérique.
Il faudrait que je prenne les pulsations de coupure pour commencer mes pentes de -20db ?
Pour la deuxième cassure
Je suis parti de Gmax-3db pour trouver la première cassure soit 23dB
Ensuite j'ai pris cette valeur et j'ai soustrait les -20dB de la première pente soit 3dB
Pour ensuite encore enlever les 3dB soit 0dB
J'imagine que ma logique n'est pas bonne mais je ne vois pas comment vous trouvez -11dB
Du coup je suis partie sur un tracé sur la période.
L'axe est soit un axe de pulsation (tracé théorique) soit un axe de fréquence (tracé pratique), d'ailleurs vous avez marqué vous-même les points remarquables 1/T1 et 1/T2, donc vous avez raisonnez en pulsation.
Sur le principe c'est juste : coupure 1/T1 et 1/T2.
Juste pour savoir si je devais faire un tracé numérique. Il faudrait que je prenne les pulsations de coupure pour commencer mes pentes de -20dB ?
C'est bien cela, il n'y qu'à remplacer 1/T1 et 1/T2 par leurs valeurs.
Pour la première cassure pas de problème.
Ensuite j'ai pris cette valeur et j'ai soustrait les -20dB de la première pente soit 3dB
20 dB c'est 20 dB par décade, donc cela aurait marché avec une décade (un facteur 10) entre les deux pulsations de coupure.
Il faut simplement prendre en compte les deux filtres : l'effet du deuxième est bien -3 dB, pour le le premier, on est sur l'asymptote donc
Ok pour la deuxième cassure, je n'avais pas pris ça en compte.
Merci pour ces explications qui me font avancer dans la compréhension de ce sujet.
Bonne soirée
Bonjour,
J'ai une autre question sur un sujet identique.
Énoncé :
Tracer le diagramme de Bode asymptotiques et esquisser la courbe réelle de la fonction de transfert (pour cela calculer les ordonnées des points de ruptures des asymptotes)
T1(jf)=(200+j.0,4.f)/(10+j.f)
J'aurais tendance à partir sur ma même idée que pour l'exercice d'avant soit une découpe en sous-ensemble
H0=(200+j.0,4.f) et H1=1/(10+j.f)
Ce qui me donne
pour f0
GHo=46dB et GH1=0
ArgHo=0 et ArgH1=0
Pour f+
GH0=pente de +20dB/décade et Gh1=pente de -20dB/décade
ArgHo=/2 et ArgH1=-/2
Fréquences de coupure:
Fc0=2.5
Fc1=1
Fc2<Fc1
J'ai plusieurs questions :
Ma logique de départ et donc mes résultats qui suivent sont-ils corrects ?
Aurais-je pu/du essayer de transformer ma fonction transfert de départ en une forme normalisé d'un filtre (1er ou 2éme ordre, passe-bas/bande/haut) ?
Merci
Aurais-je pu/du essayer de transformer ma fonction transfert de départ en une forme normalisé d'un filtre
Du peut-être pas, mais que cela soit une bonne idée c'est sûr.
Découpage : OK
Comportement continu, HF : OK
Par contre, cela ne marche pas pour les fréquences de coupure, les fréquences de coupure correspondant à (1+j*f/f0), donc sous la forme normalisée (on peut généraliser mais sous cette forme c'est quand même plus simple).
J'ai essayé de mettre ma fonction de transfert sous forme normalisé d'un filtre mais je galère un peu, j'ai bien trouvé quelque chose mais je doute sur le résultat.
(200+j0.4f)/(10+jf)
divisé par 10
(20+j0.04f)/(1+j0.1f)
20(1+j0.002f)/(1+j0.1f)
20*(1+j0.002f)/(1+j0.1f)
f1=1/0.002 et f2=1/0.1
20*(1+j*f/f1)/(1+j*f/f2)
Si vous voulez un moyen de vérifier, vous pouvez utiliser WolframAlpha 
Il faudra simplement mettre sous forme symbolique (s à la place de j*f ou j*) et que tout le reste soit numérique.
Dernière question sur le sujet :
Enoncé:
Déterminez le signal de sortie s(t) du filtre sachant que:
e(t=Eo+Eosin(t)
Avec Eo=5V et f=10kHz
Pour f=10kHz le Gain=-10dB et la Phase=1.5rad
Je sais que s(t)=H(t)xe(t) et que G=log(|H|)
Donc -10=20log(|H|)
log(|H|)=-1/2
|H|=10*-1/2=0.31
Donc H=[0.31;1.5]
Après j'aurais tendance à faire :
s(t)=0.31*5+0.31*5sin((t-1.5)t)
s(t)=1.55+1.55sin((-1.5)t)
Je pense que le début est bon par contre la partie après le sinus doit être fausse ?
Bonjour,
"Je sais que s(t)=H(t)xe(t) ", plutôt , pour bien rappeler que c'est uniquement pour la composante sinusoïdale à la pulsation
.
Il faut donc traiter séparément la partie continue et la partie sinusoïdale.
Comment avez-vous trouvé le gain et la phase ?
Je ne trouve pas cela pour 10 kHz.
Il faut notez que 10 kHz est grand vis-à-vis des deux fréquences de coupure et que l'on peut considérer qu'on se trouve sur l'asymptote HF.
Désolé, j'ai mal expliqué ce problème et j'ai oublié de mettre le diagramme de Bode correspondant. C'est un nouvel exercice qui n'a pas de rapport avec mes questions précédentes. C'est juste que c'était dans le même thème du coup j'ai continué sur ce sujet.
Enoncé complet :
On applique en entrée de ce filtre le signal e(t=Eo+Eosin(t)
avec E0=5V et f=10kHz
De plus je n'avais pas mis le diagramme de Bode correspondant à cet exercice, désolé.
Réponse :
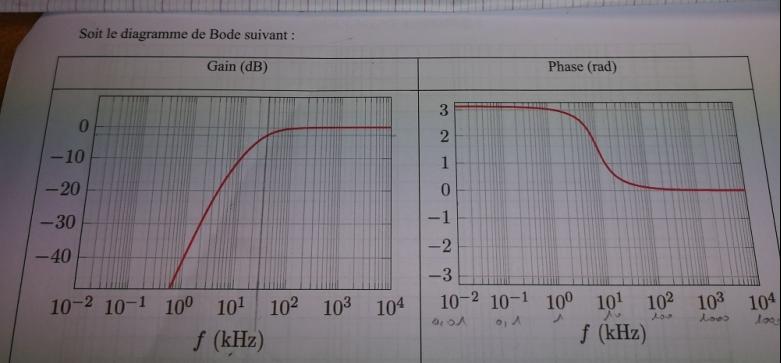
D'après le diagramme de Bode je sais que pour f=10kHz
G=-10dB et Phase=1.5rad
Du coup, j'ai calculé H pour f=10kHZ soit 0.31
S(=H()*E()
C'est ici que je bloque après ?
OK compris,
Votre calcul est donc correct pour 10 kHz : la partie sinusoïdale vaut bien 1.55 sin(t+1,5) (1,5 est la phase donc pas en facteur avec t et vaut +1,5 et non -1,5.
Pour la partie continue, il faut prendre le gain BF, or vous avez manifestement un passe-haut (donc gain nul en continu), il n'y a donc pas de continu dans le signal de sortie.
Annuler
connectez vous
en post-bac