1) Valeurs de R₁, R₂, L et C
Designons par :
cos₁ le facteur de puissance de D₁ ;
cos₂ le facteur de puissance de D₂ ;
cos le facteur de puissance de l'ensemble.
D'après l'énoncé :
• cos₁=cos, alors tan₁=tan
Soit
Ce qui conduit à   (relation 1)
• Aux bornes de l'ensemble :
Or Z = U/I = 12/0,5 = 24
Alors
J'obtiens   (relation 2)
• Aux bornes de D₂ : cos₂ = R₂/Z₂ ½=R₂/Z₂ Z₂=2R₂
Donc
J'obtiens   (relation 3)
• Toujours aux bornes de l'ensemble :

Or Z=24 et R₁+R₂=123
J'obtiens   (relation 4)

Maintenant,  quand je combine ces 4 relations,
je trouve
R₂=0 (ce qui me paraît illogique)
R₁=123  
Aidez-moi svp

Bonjour
As-tu réalisé le diagramme de Fresnel correspondant à la situation ? Tu devrais constater que nécessairement :


₁=30°
₂=-60°
= -30°

Il y a de bonnes choses dans ce que tu as écrit mais aussi plusieurs signes à corriger.

D'accord
• Aux bornes de D₁, on a :
cos30⁰ = R₁/Z₁
Or
En remplaçant Z₁ par son expression, J'obtiens :
  (relation 1)
• Aux bornes de D₂, on a :
cos(-60⁰) = R₂/Z₂
En remplaçant cos(-60⁰)=½ et Z par J'obtiens :
  (relation 2)
•Aux bornes de l'ensemble, on a :


Or Z =U/I = 12/0,5 = 24
En remplaçant Z par sa valeur, J'obtiens

(relation 3)

D'autre part

Or
Alors J'obtiens :

  (relation 4)

En combinant ces 4 relations, je trouve


De la relation 1, je tire : L = 19 mH
De la relation 2, je tire C et je trouve
C = 176,8 F

Si c'est bon, maintenant la question 2)
a) Non
b) Oui, car les condensateur permettent de relever le facteur de puissance d'une  installation.
c) Calculons la capacité C₀ de ce condensateur :
Si facteur de puissance est égal à 1, alors =0⁰ et R₁+R₂=Z, le circuit est à la résonance.
Dans ce cas particulier LC₀² = 1
Je tire C₀ et je trouve : C₀=633 F

D'accord avec ton message du 27-04-22 à 18:12.

D'accord, mais est-ce mes réponses finales concernant la 1ère question sont correctes ?

Désolé si mon message précédent ne t'a pas paru suffisamment clair.
Oui, tes réponses à la question 1 sont correctes mais il te faut revoir la question 2 en tenant compte de mon message précédent.

D'accord, voici mon diagramme de Fresnel à la question 1)
Je ne sais pas s'il est bon, ou si je dois faire dans deux diagrammes distincts D₁ et D[sub][/sub].

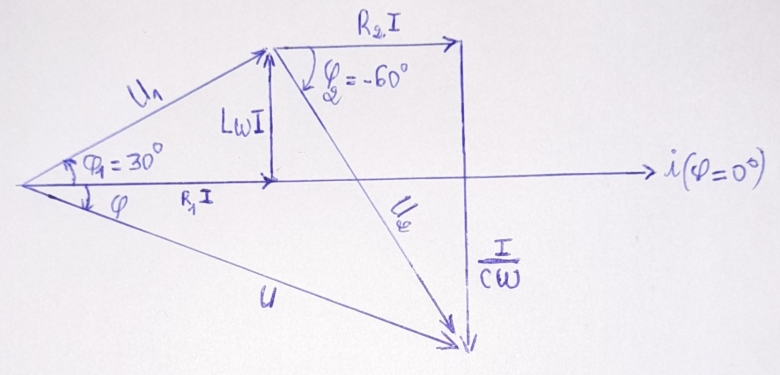
Ah si je comprend bien ce diagramme, pour porter le facteur de puissance de l'association à 1, il faudra pour ce cas particulier associer en série avec D₁ et D₂ une inductance pure.
À supposer qu'on a branché un condensateur, le décalage entre u(t) aux bornes de l'ensemble et i(t) va s'agrandir davantage, c'est-à-dire le vecteur de Fresnel s'éloignera de i(t) vers le bas.
Mais si l'on branche une self-pure cela permettra de réduire l'angle jusqu'à l'annuler.

Ci-dessous le nouveau diagramme de Fresnel où le vecteur en rouge représente le vecteur de Fresnel aux bornes de la self-pure qui porte le facteur de puissance à 1.

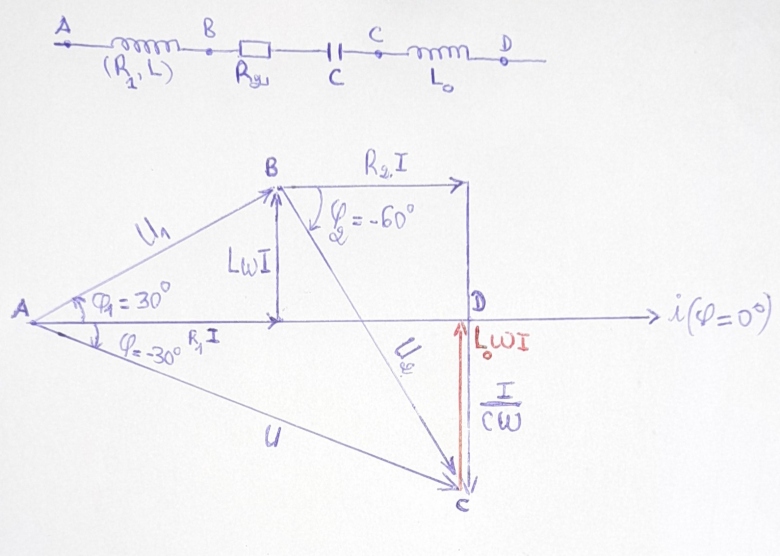
Maintenant pour calculer la valeur de L₀, je considère le triangle rectangle ADC et je pose :



Soit L₀38 mH

Tes diagrammes de Fresnel semblent indiquer que maintenant tu as bien compris.D'accord aussi avec ta valeur de L_o.
Juste une remarque : personnellement, j'arrondis tous les résultats demandés à 3 chiffres significatifs tout en gardant en mémoire les valeurs données par la calculatrice pour éviter que les arrondis successifs ne conduisent à des erreurs significatives. Cela me donne :
R₁=R₂=10,4
L=19,1mH
C=177µF
L_o=38,2mH.

Vanoise, merci bien !