Inscription / Connexion Nouveau Sujet
exercices sur les ondes mécaniques
Bonjour, je suis bloqué dans l'exercice suivant :
On dispose d'une corde de guitare tendue horizontalement, à l'altitude z=0. on déplace verticalement l'extrémité A de la corde. L'altitude Za du point A varie donc en fonction du temps selon les valeurs données dans le tableau:
t(ms) 0 ;10 ;20 ;30 ;40
Za(cm) 0 ;3 ;2 ;1 ;0
la perrtubation se déplace le long de la corde , et atteint le point P situé à une distance d= 4.00 m du point source A à la date t1 = 0.640 s
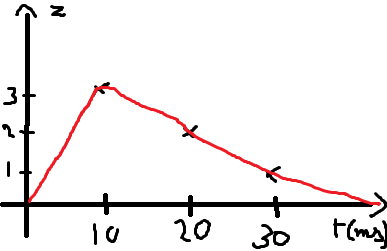
1a) représenter graphiquement les variations de l'altitude du point A en fonction du temps
b) décrire le mouvement de A.
2) calculer la valeur de la célérité Conde de l'onde progressive.
3)sur quelle longueur s'étale la perturbation sur la corde ? on se placera à une date t > 40ms
4) à quelle date le point P précédemment affecté par la perturbation se retrouve-t'il au repos ?
5a) quel point de la corde possède une altitude maximale à l'instant t1 ?
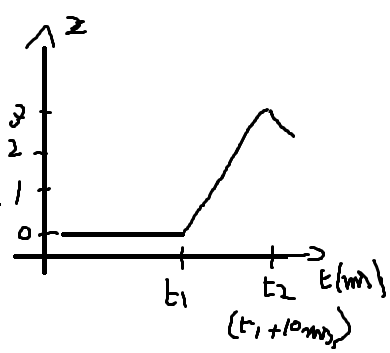
b) représenter avec soin, et en renseignant l'axe des abscisses, l'aspect de la portion de corde affecté par la perturbation à la date t1
Je ne suis pas sur du schéma que j'ai effectué pour la première question je l'ai mis dans les pièces attachées au message.
Sinon j'ai réussi toutes les questions sauf la 5ème qui me pose problème, je ne vois pas quel point pourrait posséder une altitude maximale a l'instant t1
Voilà je vous remercie d'avance pour votre aide.
J'ai répondu à chaque question:
2)La distance séparant A et P est de 4.00m pour un retard de 0.640s. On a donc: V=d/t
V=4.00/0.640=6.25 m/s
La célérité Conde de l'onde progressive est de 6.25 m/s
3) puisque t> 40ms alors le retard delta t est de 40ms on a donc : v=d/delta t
donc d= 6.25*0.040=0.25=25cm
Une perturbation qui s'étale donc sur 25 cm sur la corde
4) Le point P se trouve au repose à t1+delta t=0.68 s
Parfait !
Pour la question 5 :
Il faut maintenant combiner les résultats des questions précédentes (c'est pour cela que je voulais m'assurer qu'elles étaient bonnes)
. La perturbation est maximale 10 ms après son début...
. La perturbation progresse à 6,25 m.s-1
. À t1 = 0,640 s la perturbation atteint (tout juste) le point P
Où se trouve le maximum de la perturbation à cet instant t1 ?

1) on cherche une position, donc la réponse sera une distance et l'unité sera le mètre
2) on cherche pour cette question et la suivante (5a et 5b) ce qui se passe à l'instant t1 = 0,640 s

une perturbation correspond à 0.25m en 40ms. puisque t>40ms on retire à 4m 0.25cm ce qui donne 3.75m?
Ou bien à l'instant t1 l'altitude correspond à 0 donc pour obtenir la distance à t1 + 10 ms (qui correspond au maximum) = 0.650s on fait 4+0.25/4-0.25 =3.81m?
Ni l'un ni l'autre...
Le maximum de perturbation (voir ta courbe) se produit 10 ms après le début de la perturbation.
À t1 = 0,640 s le point P est au début de la perturbation
(Donc pour t2 = 0,650 s le point P sera au maximum de la perturbation, mais ce n'est pas la question ! )
À t1 = 0,640 s, le maximum de la perturbation n'est pas encore arrivé au point P. Mais il n'est pas loin. Il sera là dans 10 ms. La perturbation se déplace à 6,25 m.s-1. À quelle distance de P se trouve donc ce maximum ?
Et donc... quelle est son abscisse à t1 ?

Mmmm le maximum se trouve donc à : d=0.010*6.25=0.0625 donc pour t1
4.00-0.0625=3.94 metres
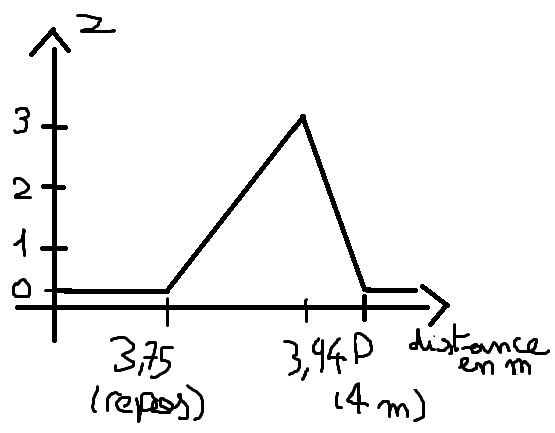
et donc pour le schéma j'obtient ça :
1) Oui, à l'instant t1 le maximum est à l'abscisse 3,937 5 m (c'est-à-dire 6,25 cm avant le point P)
2) Question 5b
Ce n'est pas ce que l'on te demande.
On te demande l'aspect de la corde au voisinage du point P à l'instant t1
Donc l'axe des abscisses ne sera plus le temps mais sera la distance, les positions
Tu sais déjà :
. que le point P (abscisse 4,00 m) n'est pas perturbé mais que c'est... tout juste !
. que le point 6,25 cm avant P est au maximum de la perturbation
. que la longueur totale de corde perturbée vaut 25 cm (donc 25 cm avant P, c'est-à-dire à 3,75 m on retrouve le repos...)
Voilà qui devrait te faciliter la vie !


Les valeurs sont bonnes ; et le dessin est faux !
Combien de centimètres entre 3,75 m et 3,9375 m ?
Combien de centimètres entre 3,9375 m et 4,00 m ?
Alors... recommence le dessin.
Et tu touches du doigt ce qui est le problème de tous les lycéens quand ils constatent cela pour la première fois dans cette partie du programme. Donc, retiens bien la solution que tu vas nous montrer maintenant !

Oui !
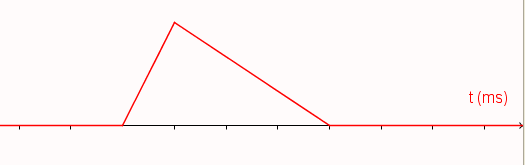
Au-dessus : en fonction du temps, l'altitude d'un seul point, quelconque, de la corde. Les graduations sur l'axe indiquent des durées de 10 millisecondes.
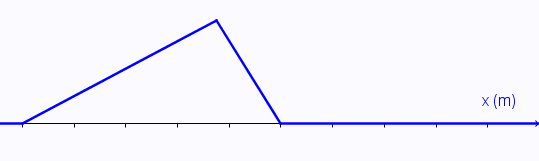
Au-dessus : en fonction de l'abscisse, l'altitude de tous les points de la corde pour un seul instant. C'est donc comme une photographie de la corde à cet instant. Les graduations sur l'axe indiquent des espaces de 5 centimètres.
Réfléchis bien à cela et retiens ! C'est un grand classique de ton programme.

J'ai utilisé GeoGebra ; même s'il est capable de bien d'autres choses.
Il y a deux logiciels (gratuits tous les deux) que chaque lycéen devrait posséder. Ils sont complémentaires :
. pour la géométrie (et en particulier la géométrie analytique) : Geogebra : 
![]()
. pour l'analyse, les statistiques... : Sine qua non : 
![]()