Niveau terminale

Exercices sur les forces

Posté par
Tangara 28-08-18 à 20:41

Bonjour à tous,

Pour me présenter brièvement et expliquer les raisons de mon inscription ici. J'ai passé mon bac il y a 15 ans. Dans le cadre d'une volonté de reconversion professionnelle, je me remets aux matières scientifiques (maths; physique; chimie), en reprenant mes cours et m'informant à gauche à droite.
J'ai une série d'exercices que j'ai compris mais certains autres bloquent d'om mon inscription. Aussi je ne cherche pas la résolution mais plutôt apprendre les formules et le raisonnement.

Par ailleurs aux modos ou aux habitués, je risque d'ouvrir plusieurs topics pour les forces de Newton et la cinématique.

Voici le premier exercice :

Une masse m=5kg démarre à une vitesse nulle à l'instant t=0s sur un plan incliné d'un angle B par rapport à l'horizontal. On pose g=10m/s² et sin B =1/2 et on considère qu'il n'y a pas de frottement. Après avoir parcouru une distance de 10m, la vitesse v de la masse vaut ?

Voila ce sur quoi je suis parti :
En lisant l'énoncé, j'en déduit que l'angle vaut 30° mais ça ne me sert pas trop

j'ai alors hésité entre chercher à connaître la vitesse à partir de l'accélération avec a = dv/dt mais j'en reste là.

J'ai aussi essayé  somme forces = ma
les forces sont P = mg = 50N = ma  d'où a=10 m/s²

Et je tourne en rond. Pouvez vous m'aider ?

Merci d'avance

Posté par re : Exercices sur les forces 28-08-18 à 21:52

Bonjour Tangara,

Félicitations pour ton courage, c'est pas évident de reprendre !

Il existe en faite plusieurs manières de résoudre cet exercice.
Tu peux en effet utiliser la relation fondamental de la dynamique et décomposer les forces dans un repère où l'axe (Ox) suit la pente et l'axe (Oy) perpendiculaire à (Ox) ira suivant la direction de la force de support $\vec{R}$ .

Cependant, je propose autre chose, nous allons appliquer le théorème de l'énergie cinétique qui dit que la variation de l'énergie cinétique est égale à la somme des travaux des forces.
On écrit $\Delta E_{c} = \sum W(\vec{F})$ .
L'expression du travail d'une force $\vec{F}$ suivant un parcours dirigé par le vecteur $\vec{AB}$ vaut $W(\vec{F}) = \vec{F}.\vec{AB} = F \times AB \times cos(\alpha)$ avec $\alpha$ l'angle entre $\vec{F}$ et $\vec{AB}$ .
L'intérêt est que la force de support est perpendiculaire au trajet $\vec{AB}$ ainsi $W(\vec{R}) = 0$ . D'après le théorème de l'énergie cinétique nous avons donc
$\frac{1}{2} m v_{B}^{2} -\frac{1}{2} m v_{A}^{2} = W(\vec{P}) = m \vec{g}.\vec{AB} = m \times g \times AB \times cos(\alpha)$ . Or la somme des angles d'un triangle étant égal à 180 degrés on sait que $\alpha = 60 degrés$ .
De plus $\vec{v}_{A}$ et $\vec{v}_{B}$ représentent respectivement la vitesse en A et la vitesse en B. L'énoncé dit bien que le corps démarre sans vitesse donc $\vec{v}_{A} = \vec{0}$ . Ainsi : $\frac{1}{2} m v_{B}^{2} = m g AB cos(60)$ .
On arrive à $v_{B} = \sqrt{2 g AB cos(60)} = 10 m/s.$

Sauf étourderie ...

Posté par re : Exercices sur les forces 29-08-18 à 08:48

Merci Kildeur pour cet eclaircissement.

cela m'aide beaucoup.
Il y a un petit hic, pourquoi prend t'on l'angle alpha plutôt que celui donné dans l'énoncé ?

Du coup pour mon raisonnement, trouver l'accélération n'est d'aucune aide ?

Posté par re : Exercices sur les forces 29-08-18 à 10:26

Citation :
Il y a un petit hic, pourquoi prend t'on l'angle alpha plutôt que celui donné dans l'énoncé ?

Non, rien de grave c'est parce que $cos(\frac{\pi}{2} - \alpha) = sin(\alpha).$
Ca revient exactement au même. J'ai juste fait un calcul numérique sur les angles avant de le mettre dans le cos .

Citation :
Du coup pour mon raisonnement, trouver l'accélération n'est d'aucune aide ?

On peut bien sûr passer par la relation fondamentale de la dynamique et chercher l'accélération selon l'axe (Ox). Tu auras dans ce cas la composante $m g sin(\alpha)$ qui apparaitre pour le poids projeté suivant l'axe (Ox).
Ensuite on a suivant l'axe (Ox) : $m g sin(\alpha) = m \frac{dv_{x}}{dt}$
d'où : $v_{x} = g sin(\alpha) t + v_{0}$ or $v_{0} = 0$ car la vitesse v = 0 en t = 0 et $x(t) = \frac{1}{2} g sin(\alpha) t^{2} + x_{0}$ avec $x_{0} = 0$ car on se place à l origine en t = 0. Avec tout ça tu devrais y arriver et tu verras que cette fois dans la formule le sinus de ton angle considéré apparait.
Pour un schéma de la situation tu le trouves facilement sur le net, c'est un exercice hyper classique. Même en tapant "plan incliné" sur wikipédia.

Posté par re : Exercices sur les forces 29-08-18 à 10:33

Bonjour,

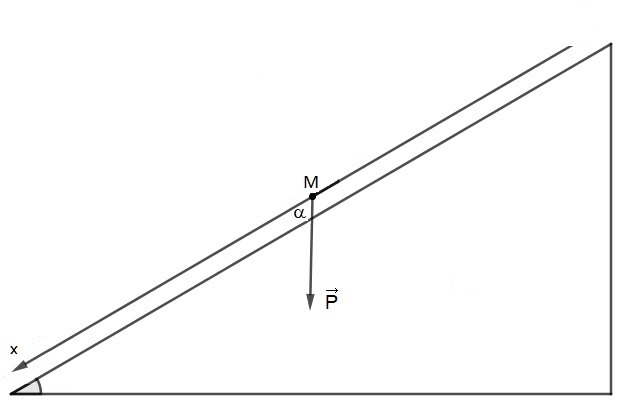
Je me permets une intrusion rapide dans les explications de Kildeur, juste pour faire profiter Tangara d'une figure que j'utilise de temps à autre et qui montre que l'angle α utilisé dans le calcul du travail du poids n'est pas l'angle du plan incliné avec l'horizontale, mais l'angle formé par la direction (orientée vers le bas) du poids et la direction orientée Mx du mouvement.

Exercices sur les forces

Posté par re : Exercices sur les forces 29-08-18 à 11:13

Merci à toi odbugt1.

Posté par re : Exercices sur les forces 29-08-18 à 12:46

Merci à vous deux ça s'éclaircit. En effet je n'avait pas saisi qu'il fallait prendre l'angle entre la force et la route et non juste l'inclinaison de la route. 4
Mon repère n'était pas bon.

Avez vous des énoncés d'exercices de ce genre pour que je m'entraine encore ?

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Exercices sur les forces

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique