Inscription / Connexion Nouveau Sujet
Exercice sur le mouvement
Bonjour,
Pouvez-vous me filer un coup de main à faire cette exercice svp :
On considère un système de masse m = 1,0*10^2kg composé d'un cycliste et de son vélo. Le système, roulant à une vitesse v0=10m.s-1, freine sur une route horizontale à partir de l'instant t=0s. Il est à l'arrêt au bout de d=5,0m. On négligera l'action de l'air et on notera vecteur F la force de frottement du sol, de norme F constante.
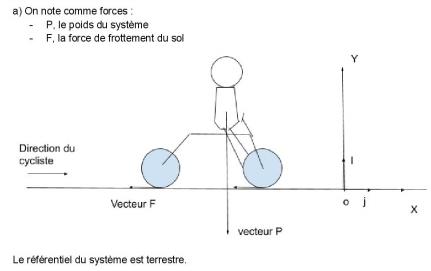
a) Faire le bilan des forces appliquées sur le système. Les représenter sur un schéma sans souci d'échelle.
J'ai mis en pièce-jointe ce que j'ai fait. J'ai juste une hésitation sur le fait de faire aussi le vecteur -P. Je ne sais pas si faut le représenter.
Et là je bloque :
b) A l'aide de la deuxième loi de Newton, déterminer les équations horaires de la vitesse et de la position du système, en fonction de F, m, v0 et du temps t.
C'est le brouillard dans ma tête, je ne vois pas où intervient la relation de Newton somme des forces = ma.
Peut-être remplacer somme des forces par F+mg et ma par mg ? mais j'en sais rien.
c) Donner l'expression de la date d à laquelle le système est à l'arrêt en fonction de F, m et v0.
d) En déduire l'expression de F en fonction de d, m et v0. Calculer sa valeur.
Voilà,
j'ai l'impression que le fait d'être bloqué à la deuxième question me "cristallise" un peu pour faire la suite de l'exo. J'aimerai vraiment le réussir..
Merci d'avance
Bonjour,
Je te conseille de lire attentivement cette fiche mise à jour pas plus tard que la semaine passée et de t'entraîner avec les applications proposées avant de revenir sur cet exercice : ![]() Statique et dynamique - Les lois de Newton
Statique et dynamique - Les lois de Newton
Tu confonds en effet les forces et les composantes des forces dans un repère ce qui est fâcheux.

Bonsoir, merci beaucoup pour la fiche.
Pour la b) si j'ai bien compris ça ressemble un peu à une question de l'exo de la luge :
a(t)=F/m
v(t)= F/m + v0
x(t) = F/m + v0t^2 + x0 où t représente le temps en seconde
Par contre pour la c) je suis toujours perdu. Sur la fiche on a un exemple où on cherche la position à un instant précis mais à quoi correspond la date ? Je ne comprends pas.
Voilà, si vous pouviez m'éclairer je suis preneur. J'ai vraiment envie de comprendre cet exercice.
Cordialement (et désolé)
Bonsoir,
Si tu as lu attentivement nos fiches de mécanique, tu as pu constater qu'un exercice de mécanique ne peut se faire sans avoir définir un référentiel d'étude, un schéma avec les forces en présence et un repère.
Peux-tu poster cela ?

Oui désolé je pensais avoir déjà mis un schéma dans mon premier post. J'espère qu'il est bon.
Désolé si le format n'est pas super, j'ai fait ça sur docs :/
J'ai encore essayé et je suis tombé sur v(t) = F/m *t +v0
Aussi je ne sais pas vraiment par rapport à mon repère mais vu que le système freine peut-être que je dois mettre une accélération négative ?
Le système est {cycliste + vélo} de masse m et de centre d'inertie G (à représenter)
Le référentiel est le sol, référentiel terrestre supposé galiléen.
Bilan des forces :
- poids du système
- les forces de frottement exercées par le sol sur le système
- la réaction du support => oubliée et à représenter !
- on négligera l'action de l'air
D'après la deuxième loi de Newton,
On projette la relation suivant l'axe (Oy)
On projette la relation suivant l'axe (Ox) tu as fait une erreur de signe lors de ta projection
Par définition de l'accélération :
avec x position du système par rapport au repère.
Alors
Avec et
constantes d'intégration.
Il faut alors utiliser les conditions initiales pour les déterminer.
Et du coup pour la c) si je dis pas de bêtise
Vélo à l'arrêt si vitesse nulle donc v(t) = (-F/m ) * t+ v0
Ah je n'avais pas vu ton dernier message, un grand merci à toi. Normalement il ne me manque plus que la dernière si j'ai bon à la c.
Vraiment, merci.
On a posté en parallèle : cf. mon message du 19-11-20 à 20:30 
Première condition initiale : à t = 0s,
donc
On a trouve l'équation régissant la vitesse
Merci beaucoup.
Est-ce que tu peux me dire si je suis bien parti pour la dernière question stp ? J'ai essayé de repartir de la réponse à la question c.
Donc j'ai :
F=((1/m) * v0) / d
Mais en appliquant le résultat final me paraît incohérent.
Est-ce que tu pourrais expliquer et justifier ce que tu fais stp ?
La physique-chimie (tout comme les maths d'ailleurs) ne consistent pas à fournir une formule magique ou un déroulé de calculs sans rédaction.

Je repars de l'équation de la position x(t)=-F/m*t^2/2+v0.t
Ça revient à dire que F=-1/m*t^2/2+v0*t
Donc F= -1/100 * 5^2/2 + 10*5 = 50N
Mais je sais que ça coince. Ça me parait bien trop faible. Je vais essayer d'y retravailler après ma journée de cours.
Désolé pour le délai de réponse.
Je repars de l'équation de la position x(t)=-F/m*t^2/2+v0.t tu n'expliques pas pourquoi ta constante d'intégration vaut B = 0
Ça revient à dire que F=-1/m*t^2/2+v0*t
Donc F= -1/100 * 5^2/2 + 10*5 = 50N pareil ici, pourquoi t = 5 s ?
Mais je sais que ça coince. Ça me parait bien trop faible. Je vais essayer d'y retravailler après ma journée de cours.
Je ne sais pas je suis perdu...
En fait je crois qu'il me faut plus que l'expression de la date à laquelle le système est totalement à l'arrêt, il faut aussi que je le calcule non ?
Parce qu'après que je connaît la valeur de t pour l'équation de ma position.
Donc je peux tout remplacer.. Mais en effet à quoi correspond exactement la constante B ? Je sais pas trop en fin de compte elle me permet juste de remonter à mon équation horaire, le principe d'intégration je crois.
Et oui en plus t n'est pas égale à 5 secondes, c'est la distance.
Donc s'il faut bien se servir de x(t) je dois utiliser ma distance finale ou initiale ? stp.
Je ne sais pas si tu as omis de recopier quelque chose de l'énoncé car il ne nous renseigne pas sur la position initiale du système.
On supposera que B = 0, le repère étant pris à la position initiale du système (ce qui n'est pas le cas sur le schéma).
Si à la distance le système est à l'arrêt à
, alors la vitesse devient nulle :
Puis dans l'équation horaire
donc tu peux remplacer par l'expression trouvée dans cette équation et en déduire
.

Ah et donc v(5) = (-F/100)*5+10=0
donc (-5F/100)=-10
-F/20 = -10 et donc F = 200 N
Un immense merci pour tout le temps et la patience que tu m'as consacré.
Juste une incompréhension qui persiste, comment peut-on dire que t=d=5,0m ?
Alors que t est en seconde d'après l'énoncé.
J'avais plus l'impression que la question juste avant, la c, a pour but de trouver la date d et du coup c'est ce d qui sert de t.
Juste une incompréhension qui persiste, comment peut-on dire que t=d=5,0m ?
Je n'ai jamais écrit une chose pareille, comment une durée (en seconde) peut être égale à une distance

J'ai l'impression que tu as des difficultés avec une écriture mathématique :
v(t) : fonction exprimant la vitesse en fonction du temps
v : t
 dx/dt
dx/dt
De même x(t) est la fonction exprimant l'abscisse de la position du système au cours du temps.
Si à la distance
Et on sait que
donc on peut écrire

Merci beaucoup pour ton explication je m'étais emmêlé les pinceaux entre distance et temps.
Donc v(ta)=0
du coup on traduit ça dans l'équation de la vitesse pour ensuite "incorporer" ce qu'on a trouvé (d) dans l'équation de la position.
Maintenant il faut que je résolve l'équation
(-F/100)*(10*(100/F)^2^/2) + 10(10*(100/F)=5 ?
ça me parait pas super évident mais si c'est bien ça je vais trouver
Désolé si je suis long à la détente c'est en grande partie de ma faute mais je n'ai rien dans mon cahier d'exo qui ressemble réellement à ce qu'on fait dans l'exercice. En tout cas merci.
Bonjour,
Merci beaucoup pour ton explication je m'étais emmêlé les pinceaux entre distance et temps.
Donc v(ta)=0
du coup on traduit ça dans l'équation de la vitesse pour ensuite "incorporer" ce qu'on a trouvé (d) dans l'équation de la position. Oui, v(ta) = 0 traduit le fait que le système est mis à l'arrêt suite au freinage) => on détermine ta puis on se concentre sur l'équation du mouvement x(ta) = d avec ta la valeur trouvée suite à la résolution de l'équation v(ta) = 0
Maintenant il faut que je résolve l'équation
(-F/100)*(10*(100/F)^2^/2) + 10(10*(100/F)=5 ? Il faut que tu fasses attention aux restitutions que tu fais sur le forum en détaillant davantage ce que tu fais, sinon on s'y perd
ça me parait pas super évident mais si c'est bien ça je vais trouver
Désolé si je suis long à la détente c'est en grande partie de ma faute mais je n'ai rien dans mon cahier d'exo qui ressemble réellement à ce qu'on fait dans l'exercice. En tout cas merci.
Pas de soucis, je te conseille de regarder aussi cette fiche qu'on vient de mettre à jour :
Je crois que c'est bon, je tombe sur F=1000N, un immense merciAs-tu fait une vérification pour t'assurer que tu retrouves bien les conditions vérifiées par les équations ?.



