Bonjour,

Bienvenue sur le forum. En vertu des règles, il faut que tu explicites ce que tu as été en mesure de faire : [***A LIRE AVANT D'AGIR***] Règles du forum

Ensuite, tu as des fiches de cours qui peuvent t'aider à avancer (clique sur la maison) : Mouvement dans un champ de gravitation

Ah oui désolé,
q1) Le référentiel géocentrique
q2) Nous pouvons supposé que les trajectoires du module et de l'ISS sont circulaires.

1. Ok
2. Ok

La suite (cf. fiche) ?

Je n'ai pas réussi la suite car je ne comprend pas comment calculer la vitesse alors que je n'ai aucun donner à part l'altitude et les minutes.

Je crois que j'ai compris, il faut utiliser v=d/t,
ce qui nous donne:
v=(2r)/t

Oui je suis en train de la regarder, elle est très bien faite merci.
Mais donc r correspond à 220km?

Je pense que m'ont professeur c'est trompé et ne nous a pas donner toutes les données nécessaire pour faire l'exercices.
Il a probablement oublier une parti de l'enoncé.

C'est peut-être parce qu'il ne faut fournir qu'une expression littérale ?

Comme proposé dans la fiche. Je te laisse étudier la fiche pour détailler comment trouver cette expression

v=d/t
ce qui nous donne:
vs=(2r)/Ts
On sait que r=R+h, d'ou:
vs=(2(R+h))/T

Encore une fois (cela te sera très sévèrement reproché le jour du bac), il faut définir ses notations !

C'est quoi v ? d ? t ? r ? h ? T ?

ah oui c'est vrai merci,
v: la vitesse en km/h
d: la distance en km
t: le temps en heure
r: le rayon en km
T: la période de révolution en heure
h: l'altitude en km

c'est correct ?

v: la vitesse du module en km/h
d: la distance séparant deux centres de graviter de deux corps A et B en km
r: le rayon de l'orbite en km
T: la période de révolution de la Terre en heure
h: l'altitude entre Soyouz et la Terre en km

Oui mais il faut adapter les notations à l'énoncé de l'exercice :

v = vitesse de Soyouz )= Vs d'après l'énoncé

d = r + h distance entre le centre de la Terre et le centre d'inertie de Soyouz
avec r le rayon terrestre (généralement noté Rt) et h l'altitude de Soyouz par rapport à la surface terrestre

T = période orbitale du module Soyouz

Et dans ces conditions, ce que tu as écrit dans ton message du 03-01-21 à 15:09 est correct

La suite ?

D'après la troisième loi de Kepler:
vs=(2r)/Ts=(G*(Mterre/r)
Ts=2*(r^3)/(G*Mterre))
ce qui nous  donne:
Ts^2=4^2*((r^3 )/(G*Mterre))
T^2/(Rterre+hs)^3=(4^2)/(G*Mterre)
Donc:
T^2/(Rterre+hs)^3=(4^2)/G*Mterre

Pareil pour T^2iss/(Rterre+hiss)^3= (4^2)/G*Mterre

Ce qui prouve que:
TS2 / (RT +hS)3 = TISS2 / (RT +hISS)3

G: constante de gravitation universelle :6,67*10^-11 N.m^2.kg^-2
Mterre: masse de la Terre en kg

Vraiment désolé si j'ai pris beaucoup de temps c'est très compliqué d'ecrire des formules.

q5) (On refait comme pour la question 3)
v=d/t
ce qui nous donne:
viss=(2r)/Tiss
On sait que r=R+h, d'ou:
vs=(2(Rterre+hiss))/Tiss

Avec:
viss : vitesse de l'ISS
d = r + h : la distance entre le centre de la Terre et le centre d'inertie de l'ISS
avec r le rayon terrestre et h l'altitude de l'ISS par rapport à la surface terrestre
T : période orbitale de l'ISS

q6) D'après la deuxième loi de Kepler :
Le segment de droite reliant le centre de gravité de la Terre et du satellite balaie des aires égales pendant des durées égales.
la valeur de la vitesse du satellite le long de sa trajectoire elliptique autour de la terre n'est donc pas constante ,elle est plus grande lorsque le satellite est proche de la terre que lorsqu'elle en est éloigné.
Donc v2>v1

je ne sais pas si c'est compréhensible

Pour écrire les formules, le plus simple sera d'apprendre à utiliser le Latex les prochaines fois :

extrait de la FAQ du forum :

Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?

Oui, cela est même encouragé.

Les correcteurs sont généralement plus attirés par un message bien écrit en Latex et bien présenté que par un message écrit avec les caractères normaux, non aéré, etc.

Le Latex est un outil mathématique qui pouvait nous permettre à tous de faciliter la lecture et la compréhension en écrivant proprement nos formules mathématiques. Nous vous invitons à prendre connaissance du guide latex présent sur le site. Un tutorial complet vous aide à faire vos premiers pas.
Bien-sûr, l'utilisation du Latex n'est pas obligatoire, mais pourquoi se priver d'un tel outil ?

Si ce langage vous semble trop compliqué à utiliser dans un premier temps, il vous est cependant possible d'insérer très simplement des caractères mathématiques dans votre texte en utilisant l'outil présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le mode d'emploi du forum.

Citation :
vs=(2r)/Ts=(G*(Mterre/r)
Ts=2*(r^3)/(G*Mterre))
ce qui nous donne:
Ts^2=4^2*((r^3 )/(G*Mterre))
T^2/(Rterre+hs)^3=(4^2)/(G*Mterre)

lilou2035584 @ 03-01-2021 à 16:27

q5) (On refait comme pour la question 3)
viss=diss/Tiss
ce qui nous donne:
viss=(2r)/Tiss
On sait que r=Rt+hiss, d'ou:
vs=(2(Rt+hiss))/Tiss

Avec:
viss : vitesse de l?ISS
diss = Rt + hiss : la distance entre le centre de la Terre et le centre d'inertie de l?ISS
avec r le rayon terrestre et h l'altitude de l?ISS par rapport à la surface terrestre
Tiss : période orbitale de l?ISS

Si on a déjà vu la 3 eme loi de Kepler en classe. Et si on sait qui est v1 et v2 grâce au schéma mais j'ai oublier de vous l'envoyer désolé

Un commentaire car je viens de m'en apercevoir : il n'est pas autorisé de poster le même exercice à plusieurs endroits en même temps :

Je te demanderai donc d'aller préciser sur l'autre site que tu reçois déjà de l'aide ici

Ah désolé je pensai qu'il n'était pas autorisé de le poster deux fois sur ce site.

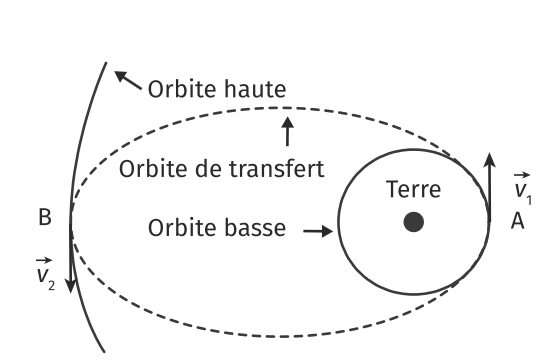
Préviens-les que tu es déjà aidé(e) ici et on continue :

extrait de la FAQ du forum :

Q03 - Pourquoi ne faut-il pas faire du ''multi-post'' ?

Pour de nombreuses raisons.

Pour mémoire, le multi-post consiste à reposer une même question dans un sujet différent , ou à poser des questions successives d'un même problème dans des sujets différents.

De même, une demande identique sur plusieurs sites sera considérée comme un multipost et la discussion pourra être fermée par un modérateur.

Etant donné tous les désagréments créés par le multi-post, le non-respect de cette règle entraînera votre exclusion temporaire ou définitive du forum !

Voici maintenant quelques raisons qui font que nous combattons avec autant d'ardeur le multi-post (et ses adeptes ) :

• La perte de temps pour les modérateurs qui consacrent leur temps bénévolement pour garantir la qualité des sujets et des échanges sur le forum.
  
• Le respect du travail des correcteurs qui consacrent leur temps bénévolement pour aider ceux qui sollicitent de l'aide.
  
• La lisibilité du forum de manière à ce qu'un sujet ayant déjà reçu de l'aide soit facilement identifié et qu'un sujet n'en ayant pas encore reçu puisse à son tour en recevoir.

Rappelez-vous une nouvelle fois la règle d'or du forum :
1 sujet créé = 1 problème

Oui pour la 6 je l'ai déjà fait, mais du coup c faux?

Au poste de 16h 43

Pour la 6 je le reformulerais plutôt ainsi et j'illustrerais les propos à l'aide d'un schéma :

D'après la deuxième loi de Kepler (ou loi des aires), le mouvement de chaque satellite est tel que le segment de droite reliant le centre de la Terre et le satellite balaie des aires égales pendant des durées égales :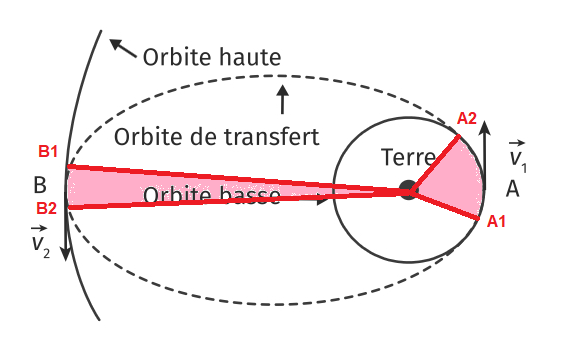



La distance A1A2 est inférieure à la distance B1B2.
Les durées de parcours entre les points A1 et A2 puis B1 et B2 sont égales.

Donc la vitesse moyenne entre les points A1 et A2 (= v1) est supérieure à celle entre les points B1 et B2 (= v2) : v1 > v2 (il y a une erreur dans ton énoncé ?)

Oui moi aussi je me suis dit que c'etait une erreur, mais j'ai vérifié et c'est bien ce qui est écrit sur mon polycopié: montrer que v2>v1.
Du coup c'est possible que ce soit une erreur venant du professeur.

Mercii beaucoup pour votre aide, je n'y serais pas arriver sans vous. Merci encore

Oui merci et désolé de vous avoir pris autant de temps je vous souhaite une bonne soirée

Ca marche, bonne soirée également et à une prochaine fois !