svp une reponse

je veux dire combien de temps parcours t il  la distance d=5m

Que signifie distance parcourue à l'instant t ???

a) "Ecart" entre la position initiale et celle à l'instant t ?

OU bien :

b) La "longueur" parcourue le long de la "route" entre l'instant initial et l'instant t ?
-----------
Autrement dit :

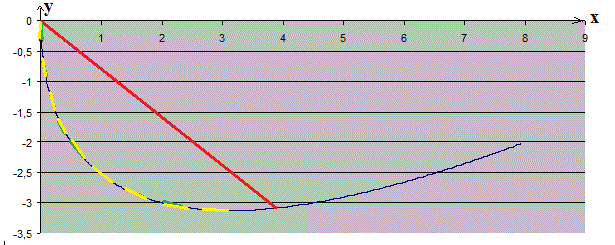
Dans le plan z = 3, on peut tracer la trajectoire du mobile y = f(x), comme la courbe en bleu sur mon dessin.

La ligne en rouge correspond à : "Ecart" entre la position initiale et celle à l'instant t égal à 5 m

La ligne en rouge correspond à : La "longueur" parcourue le long de la "route" entre l'instant initial et l'instant t égale à 5 m



Quelle est la "définition" du mot "distance" utilisé dans cet énoncé ?

On dit que le mobile est à sa position de départ à l'instant t=0

Voici le texte.                                                    Le vecteur de position dun mobile se déplaçant dans un plan muni d'un repere orthonorme (o,i,j) est OM ={x=2t,y=2t^2-5t ,z=3}.                  1) montrer que le mobile se déplace dans un plan et définir ce plan.             2)Établir l'équation cartésien de la trajectoire du mobile quel est la nature de la trajectoire ?                        3) a quel instant le mobile passe t-il au point d'abcisse x=10? Calculer la vitesse à cette instant                                4) A l'instant t=0 le mobile se trouve a son point de départ .En combien de temps parcours t-il  la distance d=5m.

Le texte est toujours aussi ambigü.

Quelle est la définition du mot "distance" dans ton cours ? (voir mon message initial)

4)

a) Si "distance" correspond au trajet jaune de mon dessin (donc pour faire comprendre : la distance parcourue le lond du trajet jaune qui correspond à la trajectoire du mobile), alors :

x'(t) = 4t
y'(t) = 4t - 5

(x'(t))² + (y'(t))² = 16t² + (4t - 5)² = 32t² - 40t + 25



1/32*[2*(8t-5)*V(32t²-40t+25) - 25*V2*argsh(1- 8t/5))](de 0 à T) = 5

1/32*[2*(8T-5)*V(32T²-40T+25) - 25*V2*argsinh(1- 8T/5) - (-50 - 25*V2*argsinh(1))] = 5

T = 1,235 s (durée cherchée arrondie)

Et le mobile est alors en (3,050 ; -3,125 ; 3)  (arrondi)
----------
b) Si "distance" correspond à "distance à vol d'oiseau", donc à la ligne rouge de mon dessin, alors :



16T^4 + 10 T² - 20 T³ = 25 (avec T > 0, mais le plus petit possible)

On trouve T = 1,386 s (arrondi)

Et le mobile est alors en (3,842 ; -3,088 ; 3)  (arrondi)
---------

J'ai bien l'impression que le niveau Terminale actuel ne permet pas de résoudre comme en "a)" ci dessus.

Il faut espérer que la définition de "distance" de ton cours correspond à la résolution b ... C'est à toi de vérifier si c'est le cas (enfin si tu as compris ce que j'essaie de dire depuis le début sur la notion de "distance").

Sauf distraction (calculs non vérifiés).  

Tentative d'éclaircissement :

A toi de savoir ce que ton prof appelle "distance", soit :

a) l'écart de position du mobile entre le départ (t = 0 s) et l'arrivée

b) la distance réellement parcourue par le mobile que ce soit en marche avant ou marche arrière ou n'importe comment.

C'est souvent la notion a qui est prise par le prof ... bien que ce n'est pas vraiment la plus judicieuse.

Avec la notion a, on obtiendrait par exemple que la distance parcourue par un voiture de F1 lors d'un grand prix est nulle ... puisque la ligne de départ et la ligne d'arrivée sont au même endroit de la piste.

Hello

Si je peux me permettre ... le fait que l'énoncé  évoque une distance "parcourue" me semble ne laisser aucune ambiguïté sur la question posée. ( cas a) de ton post du 10:44, qui est devenu le cas b) d'ailleurs à 10:49 )

Si la notion d'abscisse curviligne n'est pas au pgm de terminale, la notion de variation élémentaire et d'intégration le sont encore (pour combien de temps?)

la distance élémentaire parcourue entre t et t+dt  est v(t).dt, donc entre 0 et t la distance parcourue est d(t) = intégrale entre 0 et t de v(u)du.

J'en profite pour ma blague à 2 balles du jour:
"On dit que le mobile est à sa position de départ à l'instant t=0"
Au moins il a pas triché!  

Salut dirac,

La mise en "intégrale" du problème est facile.

Par contre, je ne suis pas sûr qu'en Terminale actuelle, on puisse la "calculer"  ... du moins l'élève moyen.

Mais c'est vrai qu'il y a longtemps que je n'ai pas regardé ce qu'il y a dans les programmes actuels.

On peut évidemment aussi résoudre le problème avec un tableur ... mais est-ce permis ?

Si tous les coups sont permis:

from math import *
d = 5.0
dt = 0.001
while l < d:
    t = t+dt
    l = l + dt*sqrt((4*t)**2+(4*t-5)**2)
print("Le temps pour parcourir ",d," est ", t)

Le temps pour parcourir  5.0  est  1.2359999999999747

la notion distance utilisée ici est lécart entre la postion initiale et la position a instant t et cest ça qu on a préciser dans lenonce     A l'instant t=0 le mobile se trouve a son point de départ

6x50=300km bien sur que oui

cest la définition de la distance dans b/ que jai tente de faire au primo mais les puissances en 4 et 3 mont pousse a arreter

Mercii beaucoup 2(J+P) bonne journée et à bientôt