Inscription / Connexion Nouveau Sujet
exercice physique
une automobile de masse 1000 kg arrive au sommet A d'une cote avec une vitesse de 36 km\h . le moteur cesse alors de fonctionner et l'auto aborde la descente AB de pente 8pour cent et de longeur 375 m .
1 - on supose qu'il n'existe aucune résistance à l'avancement ni de la part de l'air ni de la part du sol . calculer la vitesse de l'auto en B .
2 - en réalité V(b)= 65km\h . calculer l'intensité de la force;suposée constante qui équivaut aux diverse résistances à l'avancement .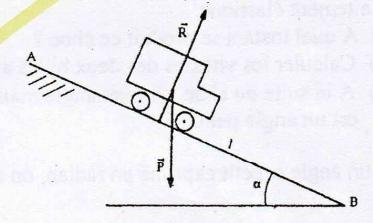
Edit Coll : forum modifié ; merci de poster dans le niveau que tu as déclaré
Bonjour 
Connais-tu le théorème de l'énergie cinétique ? Sais-tu comment calculer l'angle alpha sachant que la pente est de 8% ? Pour citer Wikipedia : "ce pourcentage se calcule en prenant la différence de hauteurs, ou d'altitudes, entre les deux extrémités du terrain concerné, divisée par la distance horizontale entre ces deux niveaux".
Ensuite, sais-tu comment calculer le travail du poids et de la réaction normale du support entre A et B ? La valeur de l'un de ces travaux est très facile à déterminer.
Tu pourras alors facilement déduire la réponse à la question 1). Et nous pourrons ensuite passer à la question 2)
Florian
oui d'après le théorème de l'enérgie cinétique j'ai trouvé que : V(b) = la racine de : 2 g
g AB
AB cos( (pisur 2) -
cos( (pisur 2) -  ) + ( v(A)
) + ( v(A) v(A)
v(A)
ms je n'arrive pas a savoir la valeur de  parceque dans l'énnoncé il n'ya pas les valeurs de : dénivré et longueur à l'horizental
parceque dans l'énnoncé il n'ya pas les valeurs de : dénivré et longueur à l'horizental
On est d'accord, on a bien :
Pour la pente à 8%, voilà comment on peut la représenter comme sur la figure ci-dessous. Peux-tu alors en déterminer la valeur de l'angle ?
Indique ensuite aussi la valeur de ton application numérique afin que je (ou un autre membre de l'île) puisse vérifier ton résultat 
Pour la question 1), je trouve une valeur différente de la tienne :
- g = 9,81 m/s²
- = sin-1(0,08)
Je trouve alors : v(B) = 26,2 m/s = 94,5 km/h
Ensuite pour la question 2) :
On te dit qu'en réalité la vitesse en B n'est que de 65 km/h. Cela est dû aux différences forces de frottement qui s'exercent sur la voiture (frottements au niveau du contact entre la route et les pneus, frottements de l'air sur la voiture). On te dit que l'on représente l'ensemble de ces forces par une force constante.
On peut supposer que cette force peut être représentée par un vecteur parallèle à la direction du déplacement de la voiture mais dans le sens inverse à ce déplacement (afin que le travail des forces soit résistant).
Peux-tu alors donner l'expression de la différence d'énergie cinétique entre A et B dans ce cas (en utilisant à nouveau le théorème de l'énergie cinétique) ?
J'ai essayé de te représenter ci-dessous la situation. Le bloc vert clair correspond à la voiture. Les vecteurs P et R correspondent au poids et à la réaction du support que tu connais. Le vecteur correspond à la force F dont tu cherches à déterminer l'intensité (tu vois bien que le vecteur est parallèle à la route).


