Inscription / Connexion Nouveau Sujet
Exercice Physique
Bonjour à tous ! Je bloque sur un exercice de physique , et je cherche un peu d'aide ici car je n'en ai pas trouver ailleurs ^^
Voici l'énoncé :
" Avec deux émetteurs et un récepteurs ultrasonores on réalise un montage. Les émetteurs sont branchées sur le même GBF. Le récepteur est relié a la voie 1 d'un oscilloscope. dans les conditions de l'expérience , la longueur d'onde des deux ondes est de 
= 8,0 mm
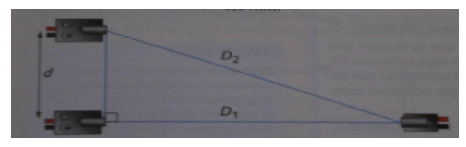
Voici le schéma ci joint.
a) Quelle relation les distances D1 et D2 doivent elles vérifier pour que la courbe observée sur l'oscilloscope ait une amplitude maximale ?
b) en déduire la distance d minimale entre les deux émetteurs dans le cas ou D1 = 20 cm
C) Même question que a) pour une amplitude minimale
Merci d'avance pour une aide quelconque ! Je ne suis pas fainéant , j'ai juste manquer les cours au moment de cette partie et je n'ai vraiment pas tous compris ^^
Cordialement !
Bonjour,
Si tu as été absent, la première chose à faire est d'apprendre ton cours...
Les franges brillantes correspondent à une différence de marche égale à un multiple entier de longueurs d'onde.
|
| = k.
avec
k 
J'ai appris mon cours avec mon livre , donc k= 1/2 or k n'est pas un entier naturel donc ce sont des amplitudes destructives , c'est bien ça ?
Désolé je me suis tromper de post ... Je n'emmêle ...
Oui donc , je disais que j'ai appris mon cours avec mon livre , mais pour la question a) par exemple , une amplitude maximale ( superposition des deux ondes en un point ) correspond a des interférences constructives.
Je pense qu'il va falloir utiliser Pythagore dans cet exercice mais je ne vois pas la relation avec D1 et D2 ..
Oui, il va falloir utiliser le théorème de Pythagore.
Que vaudra D2 pour la première amplitude maximale ?
Oui, cela c'est le théorème de Pythagore. Mais pour l'instant la physique est absente...
Que vaut D2 pour la première amplitude maximale (et c'est avec la physique des interférences qu'il faut répondre...)
Pour avoir une amplitude maximale il faut que que les deux ondes soit en phases , mais je ne vois toujours pas le relation de la question a) ...
Oui... et pour que les deux ondes soient en phase il faut que la différence de marche D2 - D1 soit égale à ...
la différence de marche devrait être égale à kx avec k un entier naturel pour qu'il y est une amplitude maximale , c'est bien ça ?
Donc D2 = 8 + 200
= 208 mm
= 20,8 cm
et d'après le théorème de phytagore d² = D2² - D1²
= (20,8)² - ( 20 )²
= 32,64 cm
Donc d = 
32,64
5,7 cm
Est-ce juste ?
pour l'amplitude minimale , il faut que la différence de marche soit égale à ( k + 1/2 )
Donc pour la première amplitude minimale D2-D1 = ( 1 + 1/2 ) x ?
Non, cela sera la deuxième amplitude minimale...
La première amplitude minimale sera évidemment pour :
D2 - D1 = [0 + (1/2)]
= / 2
0,5 : 1ère amplitude minimale
1 : 1ère amplitude maximale
1,5 : 2ème amplitude minimale
2 : 2ème amplitude maximale
2,5 : 3ème amplitude minimale
etc.
Annuler
connectez vous