Inscription / Connexion Nouveau Sujet
exercice mouvement d'un projectile
Bonjour, je suis bloqué a un exercice, voici l'ennoncé:
Un skieur de masse m,decide de franchir l'espace entre 2 tramplins symetrique.
AH = 10m
angle=30°
V0=20m/s
g=10ms
pas de frottement
et voici le schéma: 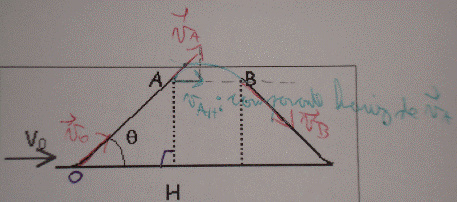
1. Quelle est la composante horizontale de la vitesse en A?
Je l'ai indiqué sur le schema mais je ne vois pas vraiment comment on calcule ca, d'ailleur j'avoue ne pas vraiment comprendre se qu'est réellement cette composante horizontale bien qu'elle soit indiquée sur le dessin 
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
C'est un problème de conservation de l'énergie mécanique : puisqu'il n'y a pas de frottements, l'énergie mécanique se conserve.
Comme , il vient :
et
.
Le vecteur est comme tu l'as dessiné. La composante horizontale vaut :
g en m/s² et pas en ms !!!!!!!!!!!
Conservation de l'énergie mécanique sur le trajet OA :
(1/2).m.Vo² - mg AH = (1/2).m.VA²
(1/2).Vo² - g AH = (1/2).VA²
(1/2)*10² - 10*10 = (1/2).VA²
VA = 7,746 m/s
VAH = VA*cos(theta)
VAH = 7,746 * cos(30°) = 6,7 m/s
-----
Sauf distraction. 
merci, j'avais utilisé la formule de l'energie cinetique entre O et A mais par contre je trouve Va=14,1m/s
donc dés qu'on a trouvé Va en gros on juste a utiliser de la trigo dans le triangle que cela forme avec Vah c'est ca?
dernière question a quoi sert cette composante horizontale? comment la détermine t-on sur le schéma?
Distraction, dans mes calculs.
1/2).m.Vo² - mg AH = (1/2).m.VA²
(1/2).Vo² - g AH = (1/2).VA²
(1/2)*20² - 10*10 = (1/2).VA²
VA = 14,14 m/s
VAH = VA*cos(theta)
VAH = 14,14 * cos(30°) = 12,2 m/s
Cette composante (VAH) permettra de calculer la longueur AB ... après avoir calculé le temps que met le skieur pour repasser, lors de sa descente, à la même altitude que le point A.
Sauf nouvelle distraction. 
merci
en effet la 2eme question demande de calculer AB, mais en utilisant la formule de la portée de tir, qui est donc:
x=(Va².sin(2. )/g
)/g
et je trouve 17,2m
Je ne vois pas a quoi ca a servis de calculer Vah, a moins qu'il y ai plusieurs façon de faire.
Oui, comme je l'ai écrit, mais cela revient au même :
z(t) = zo + VA.sin(theta) * t - gt²/2
z(t) = zo pour VA.sin(theta) * t - gt²/2 = 0, soit donc en t = 0 (quand le mobile est en A).
soit pour VA.sin(theta) - gt/2 = 0, donc en t = t1 = 2.VA.sin(theta)/g = 2*14,14*sin(30°)/10 = 1,414 s
AB = VAH * t1
AB = 12,2 * 1,414 = 17,3 m
Sauf distraction. 


