Inscription / Connexion Nouveau Sujet
exercice meca deuxième loi de newton
Bonjour,
Dans tout le problême on négligera l'action de l'air. On prendra g=10m.s-2. On raisonnera dans un repère lié à la Terre.
On choisira comme origine des dates l'instant où les mobiles quittent le plan horizontal contenant les points O et I.
1) Une bille A assimilable à un point matériel passe en I à l'instant t=0 avec une vitesse verticale, vers le bas, de norme va=7m.s-1.
Établir l'équation horaire du mouvement de la bille.
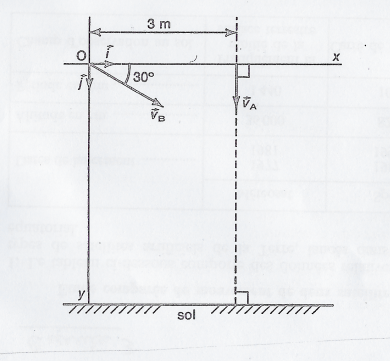
2)À l'instant t=0 on lance d'un point O une deuxième bille B, assimilable à un point matériel, dans les conditions précises sur la figure :
a) Établir l'équation horaire du mouvement projeté sur l'axe Ox ainsi que celle du mouvement projeté sur l'axe Oy.
b) Calculer la norme Vb de la vitesse initiale pour que le choc entre les deux billes se produise. Déterminer l'instant et l'endroit du choc.
Mes réponses :
1) D'après la 2ème loi de newton :
P=mg
ma=mg
a=g
2)a)
equation de la trajectoire y=f(x) On isole t :
2)b) Si je résous cela me fait deux inconnus, le temps et la vitesse
Je ne sais pas comment faire pour la 2)b)
OK
Tu as quelques erreurs dans ton développement des questions que tu as traitées.
Mais il semble que ce soient des erreurs de frappe ou d'inattention que tu devrais localiser facilement.
Pour le calcul de VB il n'est pas indispensable d'utiliser les équations que tu as établies.
Au cours de la chute, les deux balles qui sont soumises à la même accélération et qui sont initialement dans un même plan horizontal resteront dans un même plan horizontal ( donc se rencontreront) si les composantes verticales de leurs vitesses à la date t=0 sont égales.
Donc Vb*sin(α) = Va
Vb = Va / sin(α) = 7/0,5 = 14 m/s
Tu as quelques erreurs dans ton développement des questions que tu as traitées.
Mais il semble que ce soient des erreurs de frappe ou d'inattention que tu devrais localiser facilement.
Vous parlez d'erreurs de projection je suppose?
Oui.
Par exemple en me référant à ton schéma :
L'axe Oy est orienté vers le bas, le vecteur accélération de la pesanteur également donc il ne faut pas écrire que sa projection est " -g "
Je n'ai pas tout vérifié.
Je te laisse ce soin.
1) D'après la 2ème loi de newton :
P=mg
ma=mg
a=g
2)a)
equation de la trajectoire y=f(x) On isole t :
Remarque :
Il est inutile d'établir l'équation de la trajectoire de B
Quand les billes se rencontrent on a nécessairement x(A)=x(B) et y(A)=y(B)
C'est suffisant pour trouver la date tR et la position (xR , yR) de cette rencontre.
Oui effectivement c'est bien marqué équation horaire dans le sujet et non équation de la trajectoire, j'ai confondu les deux.