Inscription / Connexion Nouveau Sujet
Exercice de mécanique: mouvement d'un pendule.
Bonjour à tous et à toutes, je sollicite vos compétences afin de confirmer, ou infirmer, ma résolution de l'exercice joint ci-dessous.
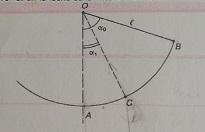
Question a:Système étudié: le pendule de masse M= 0,05kg assimilé à son centre d'inertie G dans référentiel terrestre supposé galiléen (R.T.S.G)
On utilise le théorème de l'énergie cinétique (T.C.I) pour trouver la vitesse du système au point C, en sachant que la vitesse initiale
:
On trouve que et, de la même manière,
Soit .
Même méthode pour la vitesse en a sauf qu'aucune vitesse ne s'annule. Je passe les étapes intermédiaires:
. Or,
, donc
.
Question b: Bilan des forces: Tension du fil et poids
du pendule.
On voit que , donc d'après la relation fondamentale de la dynamique (R.F.D):
.
Cette relation vectorielle étant inutilisable, on décompose dans la base de Frénet selon
, puis l'on projette les deux forces sur un axe
.
En remarquant que sur
, on obtient:
.
Question c: La méthode est identique, bien que n'ait pas besoin d'être projeté car il est porté par l'axe.
Par conséquent, .
Nota bene: Je n'ai pas tenu compte de car j'ai lu, sur ce même forum, que la tension du fil ne travaillait jamais, n'est-ce pas?
** énoncé effacé ; image laissée **
Edit Coll : merci de faire l'effort de recopier ton énoncé sur le forum 
![]()
Tu as oublié le tenir compte des racines carrées dans certains calculs numériques ... et dobc des erreurs.
a)
1/2.m.vC² = mg(hB - hC)
VC² = 2g.(hB - hC)
VC² = 2g * L(1 - cos(alpha0) - (1 - cos(alpha1)))
VC² = 2g * L(cos(alpha1) - cos(alpha0))
VC = racinecarrée[2g * L(cos(alpha1) - cos(alpha0))]
VC = racinecarrée[2 * 9,8 * 1 * (cos(25°) - cos(70°))] = 3,3 m/s
---
VA = racinecarrée[2g * L(cos(0) - cos(alpha0))]
VA = racinecarrée[2 * 9,8 * 1(1 - cos(70°)] = 3,5911 m/s arrondi à 3,6 m/s
-----
b)
TC = m.g.cos(alpha1) + m.VC²/L
TC = 1 N
-----
c)
TA = mg + m.VA²/L
TA = 0,05 * 9,8 + 0,05 * 3,5911²/1 = 1,13 N
-----
Sauf distraction. 
Merci de votre aide, J-P. Effectivement, j'aurais dû relire mes calculs, ce que je n'avais pas fait.
Cela dit, je pensais que mon raisonnement était erroné de bout en bout aussi. ^^ J'ai trouvé cet exo dans un livre du début des années 90 et, honnêtement, je ne peux retenir ma stupéfaction devant ce que l'on demande au lycée actuellement.
Les professeurs sont encouragés à débattre des phénomènes physiques avec leurs élèves, mais pas à les étudier. En voyez-vous l'intérêt, lorsque que l'on sait que malgré de passionnantes discussions, les lois de Newton, par exemple, ne changeront pas?
Attention quand tu dis "les lois de Newton ne changeront pas" ou propos du même ordre.
Certes, on continue à appliquer les lois de Newton dans des problèmes comme celui posé ici (gravitation).
Cependant, la théorie de la gravitation de Newton n'est pas compatible avec la théorie de la Relativité restreinte d'Albert Einstein. En effet, la théorie de Newton suppose des actions à distance (force de gravitation) se propageant instantanément, alors que le théorie de la Relativité restreinte précise que des actions à distance ne peuvent pas se "propager" plus vite que la vitesse de la lumière.
Et si on essaie de remettre, dans la théorie de Newton les "délais" nécessaires dans l'action à distance de la force se gravitation pour devenir compatibles avec la RR ... et bien cela ne colle pas mieux avec les observations.
C'est pour "lever" cette incompatilité entre la théorie de la gravitation de Newton et la théorie de la RR que Albert a cogité et sorti une autre théorie de la gravitation (la Relativité Générale).
Dans cette théorie la force de gravitaion imaginée par Newton n'existe plus, elle est remplacée par la notion de déformations de l'espace temps par les énergies et masses en mouvement. Les déformations de l'espace-temps se propageant à la vitesse de la lumière, mais ne la dépassant pas).
Cette théorie (la RG) n'a plus aucune incompatibité avec la RR et donne des résultats plus proches que celle de Newton par rapports aux observations pour la gravitation.
Donc la théorie de Newton, que tu pensais immuable, est prise en défaut par la RR et a été replacée par une autre théorie différente (la RG).
Pourquoi alors encore enseigner la théorie de la gravitation de Newton qu'on sait fausse ?
Et bien parce que les résultats obtenus en l'appliquant sont assez proches de ce qu'on peut observer.
Il y a des différences entre résultats des calculs et observations, mais dans la plupart des cas où les vitesses qui entrent en jeu sont très petites devant la vitesse de la lumière, les différences (calcul versus observations) sont petites et peuvent souvent être acceptables pour ce qu'on veut en faire.
De plus, la théorie de la RG (qu'on sait plus proche de ce qui est observé) est extrèmement complexe à employer, les calculs et même la simple compréhension de la théorie sont tout à fait inabordables pour la plupart des non physiciens plus que chevronnés.
Donc : La théorie de Newton, même reconnue "dépassée", est appliquée si on peut se contenter des petites imprécisions qu'elle donne.
Si on a besoin de plus de précision, on applique la RR, mais c'est vraiment réservé aux pros par son niveau de complexité.
-----
Tout ce laïus pour dire qu'en Physique, aucune théorie n'est considérée comme immuable.
Elle reste valable tant que l'observation ne la contredit pas dans certains cas.
Et s'il y a contradiction(s), soit en essaie de mettre des "rustines" à la théorie pour la rendre compatible, soit on restreint son domaine d'application, soit on tente de trouver une nouvelle théorie englobant la précédente mais capable d'expliquer aussi les cas "non conformes" découverts.
Ce n'est peut-être pas le genre de réponse que tu attendais.

Zut, dans mon message, lire :
Si on a besoin de plus de précision, on applique la , mais c'est vraiment réservé aux pros par son niveau de complexité

En réalité, je savais que vous m'exposeriez la décohérence entre la relativité générale et la mécanique newtonienne, exemple fort pertinent quand on sait que la communauté des physiciens s'acharne, sans grand succès jusqu'à présent, à concilier ces deux modèles afin de créer une théorie unifiée.
C'est bien l'objectif des théorie des cordes ou autres multivers, n'est-ce pas?
Les physiciens du XXI siècle, semblent pour la plupart, me semble t-il, accepter avec enthousiasme ou résignation, c'est selon, le fait que la science est infinie et ne cessera jamais de s'écrire, puis se réécrire, ligne après ligne, formule après formule.
Vous dites qu'aucune théorie physique ne saurait être considérée comme absolument vraie, dois-je en conclure que vous adhérez aux thèses de Karl Popper? 
Les bienfaits de l'enseignement des lois de Newton sont, eux, incontestables. Elles permettent une approche en douceur des lois physiques, tandis que la RG semble franchement complexe à saisir. Pas inabordable, mais complexe.
La théorie des cordes ne tente pas de concilier la théorie de la RG avec celle de Newton.
Elle tente d'unifier la mécanique quantique et la Relativité Générale et même au delà.
La théorie des supercordes (supersymétrie), tente une description quantique de la gravité mais aussi des autres interactions fondamentales du modèle standard et de la physique des particules.
Supercordes mais aussi super compliqué... et même si certaines avancées remarquables ont été faites dans la théorie des cordes, rien ne permet de penser que cela aboutira vraiment sur du concret.
On en parle un peu ici : ![]() et ici
et ici ![]()



