Inscription / Connexion Nouveau Sujet
Exercice de cinématique, teminale S
Bonjour ,
J'ai un exercice de physique à faire sur la cinématique et je ne comprends vraiment pas. J'ai plusieurs questions sur cet exercice mais je voudrais que quelqu'un m'aide juste pour la 1 ère question afin que je comprenne et que je puisse faire le reste s'il vous plait.
Je vous donne l'énoncé de mon exercice qui est le suivant :
Un automobiliste roule à la vitesse constante de 120 km*h sur une route rectiligne ou la vitesse est limitée à 90 km*h
Un motard de la gendarmerie part à sa poursuite. IL démarre au moment précis ou l'automobiliste passe devant lui. Il est animé d'un mouvement uniformément varié tel qu'il atteint la vitesse de 100 km*h en 10secondes.
Voici la première question :
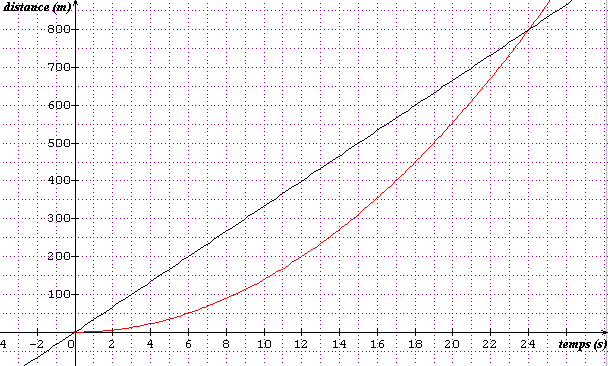
1°) déterminer la durée de la poursuite
En attente d'une réponse, s'il vous plait. Merci
Bonjour,
Attention aux unités ! L'une des clefs de compréhension de la physique...
Il ne s'agit pas de "kilomètre-heure" (dont le symbole serait km.h)
Mais il s'agit de "kilomètre par heure" dont le symbole est km/h (ou km.h-1)
_________
Il faut établir les équations horaires des deux mobiles.
Que proposes-tu ?

Merci d'avoir répondu à mon message,
alors pour l'équation horaire du motard je trouve :
v=a*t
28 = a * 10 (car 100km/h = 28 m/s)
a = 2.8
équation hhoraire du motard :
x1(t) = 1.4 *t²
Et pour l'équatiion horaire de l'automobiliste je trouve :
x2(t) = v * t
x2(t) = (120/3.6) * t
équation horaire de l'automobiliste :
x2(t) = 33.3 * t
Oui, mais tu ne trouveras pas des résultats "justes" en ayant ainsi adopté des valeurs intermédiaires arrondies
Automobiliste : x2(t) = (120/3,6) t
t
Motard : x1(t) = [100/(2 3,6
3,6 10)]
10)] t2
t2
Avec ces équations, la durée de la poursuite ainsi que la distance de la poursuite seront des valeurs "rondes"...

Je trouve donc pour la durée de la poursuite : t1 = 23.81 secondes soit 24 secondes.
Est ce que ce résultat est correct?
Ce n'est pas 23,81 secondes.
Je t'ai écrit qu'il ne faut pas utiliser ces valeurs intermédiaires arrondies.
ce qui se simplifie :
t(5t - 120) = 0
deux racines :
t = 0 s : en effet, c'est l'énoncé, pour t = 0 s le motard et l'automobiliste sont au même endroit ; l'automobiliste passe devant le motard arrêté
t = 24 s le motard rattrape l'automobiliste