Hello

Peux tu préciser là où ça coince?

1) C'est du cours. Tu le retrouves sur wikipedia si besoin

2) A Partant de cette équation, tu comprends que le nombre d'atome initial N0 est égal à le somme:

- du nombre d'atome de potassium encore présents (masse = 1,66.10^-6 g)
- et de ceux qui se sont transformés en argon (volume = 69,8.10^-4 cm³)

2) B  Là encore  fait faire appel au résultat de cours:     où est la constante de désintégration du Potassium 40 que tu détermine par la période (demi vie) qui t'es donnée:



Te voila remis en selle?

Remarque (que ne doit pas lire Hibatilez) :


Ce qui me turlupine est que :

Il y a plusieurs modes de désintégrations du K(40) :

88,8 % désintégration Beta- --> (Ca(40))
11,2 % capture d'électron --> (Ar(40))

Il semble bien que l'énoncé ne parle que de la désintégration qui donne de l'argon(40) ... qui est pourtant largement la plus petite.

Alors, on se contentant d'ajouter le nombre d'atomes de potassium encore présents et ceux qui se sont transformés en argon, on n'arrive pas à une valeur correcte de No


Voila, piqué sur Wiki  (j'ai juste copié l'isotope K(40)):

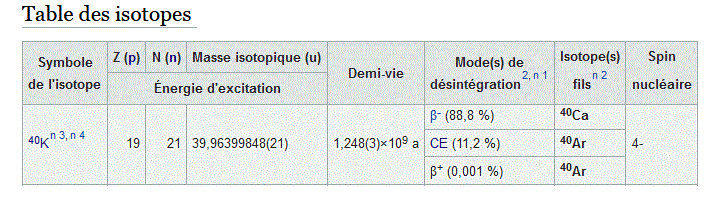
Merci infiniment .. le problème c'est qu'il s'agit pas seulement d'appliquer des règles, je veux comprendre la logique de cet exercice comme ça je vais pouvoir répondre facilement . En effet je bloque sur la dernière question . N0 désigne le potassium ou la somme de potassium et argon ?

Maintenant , après cette explication je vois mieux les choses . Merci pour votre aide M.Dirac

Hello J-P

  Dès qu'il y a le moindre truc planqué sous le tapis, il faut que cela te "turlupines".  J'avais pris soin de renvoyer Hibatilez à son cours ...

Alors ouvrons le capot.

Avec mes notations à moi:
J'appelle K le nombre d'atomes de potassium, A le nombre d'atome d'Argon

Pour en revenir à l'approche précédente, nous avions établi

   avec     t1/2 donné par l'énoncé

On aurait pu calculer A(t)  avec

   donc  

Donc



Soit



(sauf boulette de ma part comme toujours)

Donc on aurait pu truander de manière presque transparente, ne faisant plus référence à K₀

D'ailleurs on arrive numériquement à 4,3 Mds pour la Lune ce qui n'est pas mal.

Mais bon, tu as souligné que ce raisonnement n'est pas licite ...

Posons alors

_c la constante de capture électronique et _b la constante de désintégration beta- qui donne du calcium.  (la beta+ je l'ignore)

On a donc  

soit

Avec cette fois:

   donc  

Donc



Soit



Les données du problèmes fournissait = 5,5.10_-10 an^-1

Je serais curieux de savoir si une littérature fournit des données pour _c  et  _b  (j'ai rien trouvé après avoir un peu cherché)

En fait, il suffisait juste de demander à wikipedia ...



Donc mon long monologue juste pour expliquer la formule donnée à la fin de l'article wikipedia

Salut,

Voila c'est mieux ainsi.

Je sais que je j'aime bien jeter des pavés dans les mares.  

Mais il me semble que négliger, dans un énoncé, un effet (désintégration vers le Ca40) qui est environ 8 fois plus important que le seul effet mentionné (désintégration vers de l'Ar40) n'est pas très sain... cela oblige, pour arriver à une réponse finale plausible (âge de la lune),  a tricher fortement sur certaines données (teneur en Ar dans l'échantillon).

Je n'ai jamais été partisan de corriger les effets d'une erreur en en faisant  une autre.

On est souvent obligé en Physique de négliger une multitude de phénomènes pour ne pas arriver dans une étude à des choses trop compliquées ...
Mais, on ne peut négliger que des phénomènes dont les effets sur le résultat sont petits ... et évidemment pas négliger des phénomènes qui ont des effets prépondérants sur les résultats et de plus les cacher en trichant sur des données.

Mais ce n'est que mon avis.

+1