Inscription / Connexion Nouveau Sujet
Etude du lancer d'un ballon de basket.
Bonjours à tous !!
Voilà j'ai effectuer les 3 première question mais les deux autres me pose problème un coup de main me serait la bienvenue merci  !
!
Pour la Qu 1 : x= Vo cos  .t
.t
y= -1/2 gt² + Vo sin  t+yo
t+yo
z=0
Pour la Qu 2: y=(-1/2.g)(x²/Vo².cos² )+x tan
)+x tan +yo
+yo
Pour la Qu 3: Vo=  (2.g.d/sin 2
(2.g.d/sin 2 )=
)= (2*10*6025/sin (2*40)=11.26m.s-1
(2*10*6025/sin (2*40)=11.26m.s-1
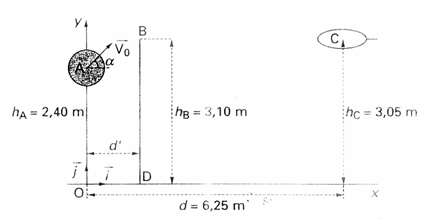
On étudie la trajectoire du centre d'inertie d'un ballon de basket-ball lancé ver le cercle du panier de l'équipe adverse par un joueur attaquant.
La résistance de l'aire est ignorée de même pour la rotation éventuelle du ballon.
Lancer vers le haut et lâcher lorsque son centre d'inertie est en A.
Données : g=10m.s-1 alpha=40° diamètre du ballon=25cm
1) Etablir les équations horaires du mouvement du centre d'inertie du ballon.
2) En déduire l'équation de la trajectoire
3) Calculer la vitesse initiale du ballon pour que celui-ci passe exactement au centre du cercle, le panier, de centre C ?
4) Un défenseur Bd placé entre l'attaquant et le panier de basket saute exactement au centre du cercle pour intercepter le ballon l'extrémité de sa main se trouve en B à l'altitude hB= 3.10 m. A quelle distance horizontale d' de l'attaquant doit-il se trouver le bas du ballon du bout des doigts ? il peut y avoir plusieurs valeurs possibles ; préciser la plus petite.
5) Quelle est la vitesse de la balle quand elle passe par le panier en C.
a) en utilisant les équations horaires.
b) Par le théorème de l'énergie cinétique.
salut
t'as fais le plus dur ....le reste c'est de l'application de la formule et des calculs mathématiques
le défenseur touche la balle ssi le pt B est sur la courbe or xB=d'
or yB=3.1 et donc avec ta formule tu déduis xB donc d'
bin oui c'est exactement ça
tu te retrouves avec une équation du second degré en x que tu résouds (2 solutions possibles surement c'est pour ça qu'on te dit dans la question plusieurs valeurs possibles...)
1)
x(t) = Vo.cos(alpha)*t
y(t) = hA + vo.sin(alpha)*t - gt²/2
-----
2)
t = x/(Vo.cos(alpha)
y = 2,4 + vo.sin(alpha)*x/(Vo.cos(alpha) - 5*(x/(Vo.cos(alpha))²
y = 2,4 + x.tg(alpha) - 5x²/(Vo².cos²(alpha))
-----
3)
Si x = 6,25, on doit avoir y = 3,05
y = 2,4 + x.tg(alpha) - 5x²/(Vo².cos²(alpha))
3,05 = 2,4 + 6,25.tg(40°) - 5*6,25²/(Vo².cos²(40°))
vo = 8,51 m/s
-----
4)
y = 2,4 + x.tg(alpha) - 5x²/(Vo².cos²(alpha))
y = 2,4 + x.tg(40°) - 5x²/(8,511².cos²(40°))
y = 2,4 + 0,839x - 0,1176x²
Si y = 3,10 + 0,125 = 3,225 -->
2,4 + 0,839x - 0,1176x² = 3,225
Il y a 2 solutions: x1 = 1,18 et x2 = 5,96
d' peut valoir 1,18 m ou 5,96 m
-----
5)
a)
x(t) = Vo.cos(alpha)*t
y(t) = hA + vo.sin(alpha)*t - gt²/2
6,25 = 8,511.cos(40°).t
t = 0,959 s
dx/dt = Vo.cos(alpha) = 6,52 m/s
dy/dt = Vo.sin(alpha) - 10t
(dy/dt)(0,959) = Vo.sin(40°) - 10*0.959 = -4,12 m/v
VC² = 6,52² + 4,12²
VC = 7,71 m/s
---
b)
(1/2).m.vo² + mg.hA = (1/2).m.Vc² + mg.hC
(1/2).vo² + g.hA = (1/2).Vc² + g.hC
(1/2).8,511² + 10.2,40 = (1/2).Vc² + 30,5
VC = 7,71 m/s
-----
Sauf distraction. 
Bonjour, j'ai moia aussi cet exercice à faire seulement je n'arrive pas à le démarrer. J'ai bien relu vos réponse mais je ne comprends pas les questions 1 et 2, pouvez vous m'expliquer?
Merci de votre aide.
On étudie la trajectoire du centre d'inertie d'un ballon de basket-ball vers le cercle du panier de l'équipe adverse par un joueur attaquant. On ne tient pas compte de la résistance de l'air ni de la rotation éventuelle du ballon.
Le lancer est effectué vers le haut ; on lâche le ballon lorsque son centre d'inertie est en A. Sa vitesse initiale est représentée par le vacteur v0 situé dans le plan ( O, i, j) et faisant un angle a avec l'axe horizontal.
g = 9,8 m s-2 ; a = 40° ; diamètre du ballon 25 cm.
Pour t=0, indiquer les valeurs litérales ou numériques des vecteurs position et vitesse.
x0 = 0 ; y0 = hA = 2,4 m ; v0x = v0 cos a = v0 cos 40 = 0,766 v0.
v0y = v0 sin a = v0 sin 40 = 0,643 v0.
Déterminer les coordonnées du centre d'inertie du ballon.
Le ballon n'est soumis qu'à son poids ; la seconde loi de Newton conduit à : ax = 0 et ay = -g.
Etablir les expressions littérales des coordonnées du vecteur vitesse et du vecteur position à une date t.
Le vecteur vitesse est une primitive du vecteur accélération :
vx = constante = v0 cos a ; vy = -gt + constante.
La constante d'intégration est déterminée par la vitesse initiale : vy = -gt + v0y =-gt + v0 sin a.
Le vecteur position est une primitive du vecteur vitesse.
x = v0 cos a t + x0 = v0 cos a t. (1)
y = -½gt2 + v0 sin a t + y0 = -½gt2 + v0 sin a t + hA. (2)
Montrer que l'expression numérique de la trajectoire dans le repère (O, i, j) s'écrit :
y = -8,36 x2/v02 +0,84 x + 2,4.
(1) donne t = x /( v0 cos a ) ; repport dans (2) :
y = -½g x2 /( v0 cos a )2 + v0 sin a x /( v0 cos a ) +hA.
y = -½*9,8 x2 /( v0 cos 40 )2 + x tan 40 +2,4.
y = -8,35 x2 / v02 + 0,84 x +2,4.



